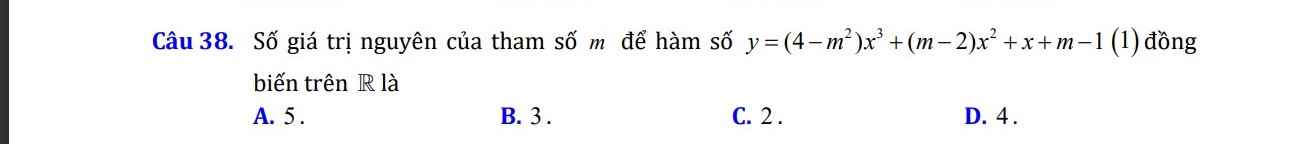- Với \(m=2\Rightarrow y=x+1\) đồng biến trên R (thỏa mãn)
- Với \(m=-2\Rightarrow y=-4x^2+x-3\) ko đồng biến trên R (ktm)
- Với \(m\ne\pm2\)
\(y'=3\left(4-m^2\right)x^2+2\left(m-2\right)x+1\)
Hàm đồng biến trên R khi: \(\left\{{}\begin{matrix}3\left(4-m^2\right)>0\\\Delta'=\left(m-2\right)^2-3\left(4-m^2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2< m< 2\\m^2-m-2\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-2< m< 2\\-1\le m\le2\end{matrix}\right.\)
\(\Rightarrow-1\le m< 2\Rightarrow m=\left\{-1;0;1\right\}\)
Vậy có 4 giá trị nguyên của m thỏa mãn
Đúng 1
Bình luận (0)
