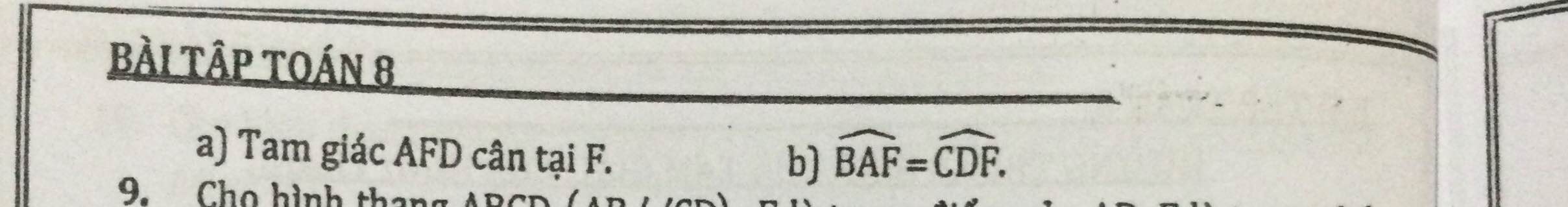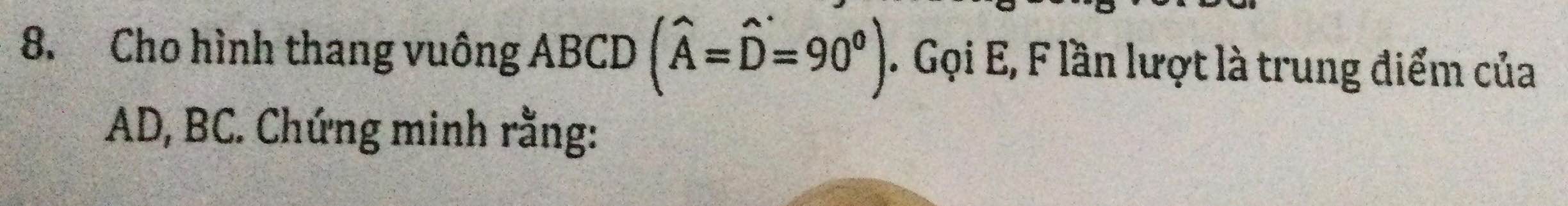a) Xét hình thang ABCD(AB//CD) có
E là trung điểm của AD(gt)
F là trung điểm của BC(gt)
Do đó: EF là đường trung bình của hình thang ABCD(Định nghĩa đường trung bình của hình thang)
Suy ra: EF//AB//DC và \(EF=\dfrac{AB+DC}{2}\)(Định lí 4 về đường trung bình của hình thang)
mà AB\(\perp\)AD(gt)
nên EF\(\perp\)AD
Xét ΔFEA vuông tại E và ΔFED vuông tại E có
FE chung
EA=ED(E là trung điểm của AD)
Do đó: ΔFEA=ΔFED(Hai cạnh góc vuông)
Suy ra: FA=FD(Hai cạnh tương ứng)
Xét ΔFAD có FA=FD(cmt)
nên ΔFAD cân tại F(Định nghĩa tam giác cân)
b) Ta có: \(\widehat{BAF}+\widehat{FAD}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)(đpcm)