Đặt \(g'\left(x\right)=2\left(x-1\right).f'\left(x^2-2x\right).\dfrac{1}{\left[f\left(x^2-2x\right)+1\right]^2}\)
Dấu của \(g\left(x\right)\) chỉ phụ thuộc dấu của \(h\left(x\right)=\left(x-1\right)f'\left(x^2-2x\right)\)
\(h\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\left(vn\right)\\x^2-2x=-1\\x^2-2x=3\end{matrix}\right.\) \(\Rightarrow x=\left\{-1;1;3\right\}\)
Bảng xét dấu \(h\left(x\right)\)
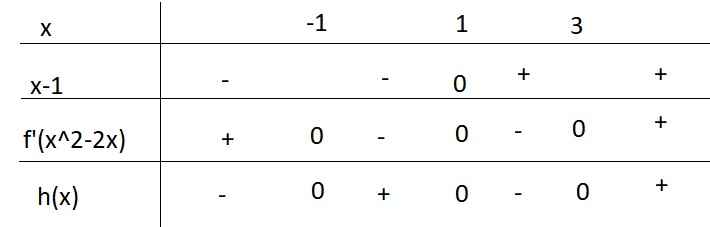
Từ bảng xét dấu ta thấy \(g\left(x\right)\) nghịch biến trên \(\left(1;3\right)\)












