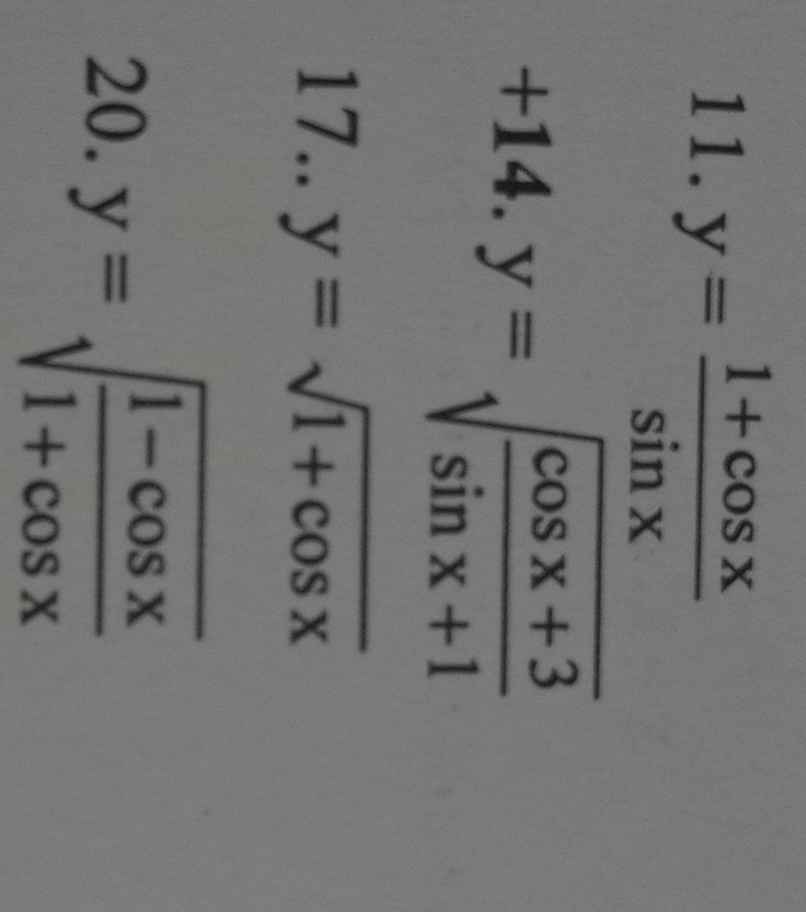11) Đk: \(sinx\ne0\Leftrightarrow x\ne k\pi\left(k\in Z\right)\)
Vậy \(D=R\backslash\left\{k\pi;k\in Z\right\}\)
14) Có \(cosx+3\ge-1+3>0\) và \(sinx+1\ge0\)
\(\Rightarrow\dfrac{cosx+3}{sinx+1}>0\) với \(sinx+1\ne0\)
Đk: \(\left\{{}\begin{matrix}\dfrac{cosx+3}{sinx+1}\ge0\\sinx+1\ne0\end{matrix}\right.\)\(\Rightarrow sinx\ne-1\) \(\Leftrightarrow x\ne-\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)
Vậy \(D=R\backslash\left\{-\dfrac{\pi}{2}+k2\pi;k\in Z\right\}\)
17) Đk: \(1+cosx\ge0\Leftrightarrow cosx\ge-1\) (lđ)
Vậy \(D=R\)
20) Có \(cosx\le1\Leftrightarrow-cosx+1\ge0\); \(cosx+1\ge-1+1=0\)
\(\Rightarrow\dfrac{1-cosx}{cosx+1}\ge0\) với \(cosx+1\ne0\)
Đk \(\left\{{}\begin{matrix}\dfrac{1-cosx}{1+cosx}\ge0\\1+cosx\ne0\end{matrix}\right.\)\(\Rightarrow cosx+1\ne0\) \(\Leftrightarrow x\ne\pi+k2\pi\left(k\in Z\right)\)
Vậy \(D=R\backslash\left\{\pi+k2\pi,k\in Z\right\}\)