Trong không gian với hệ tọa độ Oxyz, cho hai vectơ \(\overrightarrow{u}=\left(1;0;-3\right)\) và \(\overrightarrow{v}=\left(0;0;3\right)\). Hãy chỉ ra tọa độ của một vectơ \(\overrightarrow{w}\) khác \(\overrightarrow{0}\) vuông góc với cả hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\).
Bài 3: Biểu thức toạ độ của các phép toán vectơ
Luyện tập 4 (SGK Cánh Diều - Tập 1 - Trang 80)
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ overrightarrow{u}left(1;0;-3right) và overrightarrow{v}left(0;0;3right). Hãy chỉ ra tọa độ của một vectơ overrightarrow{w} khác overrightarrow{0} vuông góc với cả hai vectơ overrightarrow{u} và overrightarrow{v}.
Đọc tiếp
Thảo luận (1)
Hoạt động 4 (SGK Cánh Diều - Tập 1 - Trang 79)
a) Cho hình lập phương ABCD.ABCD có A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), C(1; 1; 1). Hãy chỉ ra tọa độ của một vectơ vuông góc với cả hai vectơb) Cho hai vectơ overrightarrow{u}left(x_1;y_1;z_1right) và overrightarrow{v}left(x_2;y_2;z_2right) không cùng phương.Xét vectơ overrightarrow{w}left(y_1z_2-y_2z_1;z_1x_2-z_2x_1;x_1y_2-x_2y_1right).- Tính overrightarrow{w}.overrightarrow{u},overrightarrow{w}.overrightarrow{v}.- Vectơ overrightarrow{w} có vuông góc với các hai vectơ overrightarrow{u} và ove...
Đọc tiếp
a) Cho hình lập phương ABCD.A'B'C'D' có A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), C'(1; 1; 1). Hãy chỉ ra tọa độ của một vectơ vuông góc với cả hai vectơ
b) Cho hai vectơ \(\overrightarrow{u}=\left(x_1;y_1;z_1\right)\) và \(\overrightarrow{v}=\left(x_2;y_2;z_2\right)\) không cùng phương.
Xét vectơ \(\overrightarrow{w}=\left(y_1z_2-y_2z_1;z_1x_2-z_2x_1;x_1y_2-x_2y_1\right).\)
- Tính \(\overrightarrow{w}.\overrightarrow{u},\overrightarrow{w}.\overrightarrow{v}\).
- Vectơ \(\overrightarrow{w}\) có vuông góc với các hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) hay không?
Thảo luận (1)Hướng dẫn giảia)

Ta có: \(\overrightarrow {AB} = (1;0;0)\), \(\overrightarrow {AD} = (0;1;0)\).
\(A'(0;0;1) \Rightarrow \overrightarrow {AA'} = (0;0;1)\).
Ta có: \(\overrightarrow {AA'} .\overrightarrow {AB} = 0.1 + 0.0 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {AB} \).
\(\overrightarrow {AA'} .\overrightarrow {AD} = 0.0 + 0.1 + 1.0 = 0 \Leftrightarrow \overrightarrow {AA'} \bot \overrightarrow {AD} \).
Vậy \(\overrightarrow {AA'} \) vuông góc với cả hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \).
b) \(\overrightarrow w .\overrightarrow u = ({y_1}{z_2} - {y_2}{z_1}){x_1} + ({z_1}{x_2} - {z_2}{x_1}){y_1} + ({x_1}{y_2} - {x_2}{y_1}){z_1}\)
\(= {x_1}{y_1}{z_2} - {x_1}{y_2}{z_1} + {y_1}{z_1}{x_2} - {y_1}{z_2}{x_1} + {z_1}{x_1}{y_2} - {z_1}{x_2}{y_1} = 0\).
\(\overrightarrow w .\overrightarrow v = ({y_1}{z_2} - {y_2}{z_1}){x_2} + ({z_1}{x_2} - {z_2}{x_1}){y_2} + ({x_1}{y_2} - {x_2}{y_1}){z_2} \)
\(= {x_2}{y_1}{z_2} - {x_2}{y_2}{z_1} + {y_2}{z_1}{x_2} - {y_2}{z_2}{x_1} + {z_2}{x_1}{y_2} - {z_2}{x_2}{y_1} = 0\).
Vậy vecto \(\overrightarrow w \) có vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 4 (SGK Cánh Diều - Tập 1 - Trang 80)
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow{a}=\left(2;-2;1\right),\overrightarrow{b}=\left(2;1;3\right)\). Hãy chỉ ra tọa độ của một vectơ \(\overrightarrow{c}\) khác \(\overrightarrow{0}\) vuông góc với cả hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\).
Thảo luận (1)Hướng dẫn giải\([\overrightarrow a ,\overrightarrow b ] = \left( {\left| \begin{array}{l} - 2\;\;\;\;1\\\;\;1\;\;\;\;\;3\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;2\\\;3\;\;\;\;\;2\end{array} \right|;\left| \begin{array}{l}2\;\;\;\; - 2\\2\;\;\;\;\;\;1\end{array} \right|} \right) = ( - 7; - 4;6)\)
Chọn \(\overrightarrow c = ( - 7; - 4;6)\) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 1 (SGK Cánh Diều - Tập 1 - Trang 80)
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow{a}=\left(2;3;-2\right)\) và \(\overrightarrow{b}=\left(3;1;-1\right)\). Tọa độ của vectơ \(\overrightarrow{a}-\overrightarrow{b}\) là:
A. (1; – 2; 1). B. (5; 4; – 3). C. (– 1; 2; – 1). D. (– 1; 2; – 3).
Thảo luận (1)Hướng dẫn giải\(\overrightarrow a - \overrightarrow b = (2 - 3;3 - 1; - 2 - ( - 1)) = ( - 1;2; - 1)\)
Chọn C
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 3 (SGK Cánh Diều - Tập 1 - Trang 80)
Trong không gian với hệ tọa độ Oxyz, cho overrightarrow{a}left(-1;2;3right),overrightarrow{b}left(3;1;-2right),overrightarrow{c}left(4;2;-3right).a) Tìm tọa độ của vectơ overrightarrow{u}2overrightarrow{a}+overrightarrow{b}-3overrightarrow{c}.b) Tìm tọa độ của vectơ overrightarrow{v} sao cho overrightarrow{v}+2overrightarrow{b}overrightarrow{a}+overrightarrow{c}.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow{a}=\left(-1;2;3\right),\overrightarrow{b}=\left(3;1;-2\right),\overrightarrow{c}=\left(4;2;-3\right).\)
a) Tìm tọa độ của vectơ \(\overrightarrow{u}=2\overrightarrow{a}+\overrightarrow{b}-3\overrightarrow{c}\).
b) Tìm tọa độ của vectơ \(\overrightarrow{v}\) sao cho \(\overrightarrow{v}+2\overrightarrow{b}=\overrightarrow{a}+\overrightarrow{c}\).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow u = 2\overrightarrow a + \overrightarrow b - 3\overrightarrow c = (2.( - 1) + 3 - 3.4;2.2 + 1 - 3.2;2.3 - 2 - 3.( - 3)) = ( - 11; - 1;13)\)
b) \(\overrightarrow v + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \Leftrightarrow \overrightarrow v = \overrightarrow a + \overrightarrow c - 2\overrightarrow b \)
\( \Leftrightarrow \overrightarrow v = ( - 1 + 4 - 2.3;2 + 2 - 2.1;3 - 3 - 2.( - 2)) = ( - 3;2;4)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5 (SGK Cánh Diều - Tập 1 - Trang 81)
Trong không gian với hệ trục tọa độ Oxyz, cho \(\overrightarrow{a}\) = (3; 2; -1), \(\overrightarrow{b}\) = (-2; 1; 2). Tính côsin của góc \(\left(\overrightarrow{a},\overrightarrow{b}\right)\).
Thảo luận (1)Hướng dẫn giải\(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}} = \frac{{3.( - 2) + 2.1 - 1.2}}{{\sqrt {{3^2} + {2^2} + {{( - 1)}^2}} .\sqrt {{{( - 2)}^2} + {1^2} + {2^2}} }} = \frac{{ - \sqrt {14} }}{7}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 7 (SGK Cánh Diều - Tập 1 - Trang 81)
Cho hình hộp ABCD.ABCD, biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác overrightarrow{0} vuông góc với cả hai vectơ trong mỗi trường hợp sau:a) overrightarrow{AC} và overrightarrow{BD};b) overrightarrow{AC} và overrightarrow{BD}.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D', biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C'(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác \(\overrightarrow{0}\) vuông góc với cả hai vectơ trong mỗi trường hợp sau:
a) \(\overrightarrow{AC}\) và \(\overrightarrow{B'D'}\);
b) \(\overrightarrow{AC'}\) và \(\overrightarrow{BD}\).
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {AB} = (1;1;1),\overrightarrow {AD} = (0; - 1;0)\)
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {AC} = (1;0;1\))
\(\overrightarrow {B'D'} = \overrightarrow {BD} = ( - 1; - 2; -1 )\)
\([\overrightarrow {AC} ,\overrightarrow {B'D'} ] = \left( {\left| \begin{array}{l}\;\;\;0\;\;\;\;1\\ - 2\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;1\\\;-1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;\;0\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = (2; 0;- 2)\)
Chọn \(\overrightarrow u = (2; 0; - 2)\) vuông góc với cả hai vecto \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \).
b) \(\overrightarrow {AC'} = (3;5; - 6)\), \(\overrightarrow {BD} = ( - 1; - 2; - 1)\)
\([\overrightarrow {AC'} ,\overrightarrow {BD} ] = \left( {\left| \begin{array}{l}\;\;\;5\;\;\;\; - 6\\ - 2\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l} - 6\;\;\;\;\;\;3\\\; - 1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}3\;\;\;\;\;\;\;5\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = ( - 17;9; - 1)\)
Chọn \(\overrightarrow v = ( - 17;9; - 1)\) vuông góc với cả hai vecto \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 8 (SGK Cánh Diều - Tập 1 - Trang 81)
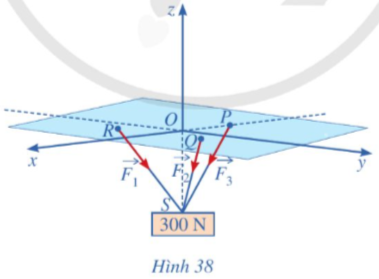
Một vật có trọng lượng 300 N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trong các điểm Pleft(-2;0;0right),Qleft(1;sqrt{3};0right),Rleft(1;-sqrt{3};0right) còn đầu kia gắn với vật tại điểm Sleft(0;0-2sqrt{3}right) như Hình 38. Gọi overrightarrow{F_1},overrightarrow{F_2},overrightarrow{F_3} lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ của các lực overrightarrow{F_1},overrightarrow{F_2},overrightarrow{F_3}.
Đọc tiếp
Một vật có trọng lượng 300 N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trong các điểm \(P\left(-2;0;0\right),Q\left(1;\sqrt{3};0\right),R\left(1;-\sqrt{3};0\right)\) còn đầu kia gắn với vật tại điểm \(S\left(0;0-2\sqrt{3}\right)\) như Hình 38. Gọi \(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\) lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ của các lực \(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\).
Thảo luận (1)Hướng dẫn giảiTa có: \(\mathop {SP}\limits^ \to = ( - 2;0;2\sqrt 3 ),\mathop {SQ}\limits^ \to = (1;\sqrt 3 ;2\sqrt 3 ),\mathop {SR}\limits^ \to = (1; - \sqrt 3 ;2\sqrt 3 )\).
Suy ra: \(\left| {\mathop {SP}\limits^ \to } \right| = \left| {\mathop {SQ}\limits^ \to } \right| = \left| {\mathop {SR}\limits^ \to } \right| = 4\).
Mặt khác: \(\mathop {SP}\limits^ \to = (3;\sqrt 3 ;0),\mathop {QR}\limits^ \to = (0; - 2\sqrt 3 ;0),\mathop {SR}\limits^ \to = ( - 3;\sqrt 3 ;0)\).
Suy ra: \(\left| {\mathop {QP}\limits^ \to } \right| = \left| {\mathop {QR}\limits^ \to } \right| = \left| {\mathop {RP}\limits^ \to } \right| = 2\sqrt 3 \) nên tam giác PQR đều.
Do đó: \(\left| {\mathop {{F_1}}\limits^ \to } \right| = \left| {\mathop {{F_2}}\limits^ \to } \right| = \left| {\mathop {{F_3}}\limits^ \to } \right|\). Tồn tại hằng số \(c \ne 0\) sao cho:
\(\mathop {{F_1}}\limits^ \to = c\mathop {SR}\limits^ \to = (c; - \sqrt 3 c;2\sqrt 3 c)\)
\(\mathop {{F_2}}\limits^ \to = c\mathop {SQ}\limits^ \to = (c;\sqrt 3 c;2\sqrt 3 c)\)
\(\mathop {{F_3}}\limits^ \to = c\mathop {SP}\limits^ \to = ( - 2c;0;2\sqrt 3 c)\)
Suy ra \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = (0;0;6\sqrt 3 c)\).
Mà \(\mathop {{F_1}}\limits^ \to + \mathop {{F_2}}\limits^ \to + \mathop {{F_3}}\limits^ \to = \mathop F\limits^ \to \), trong đó \(\mathop F\limits^ \to = (0;0; - 300)\) là trọng lực của vật.
Suy ra \(6\sqrt 3 c = - 300\), tức \(c = \frac{{ - 50\sqrt 3 }}{3}\).
Vậy \(\mathop {{F_1}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3};50; - 100} \right),\mathop {{F_2}}\limits^ \to = \left( {\frac{{ - 50\sqrt 3 }}{3}; - 50; - 100} \right);\mathop {{F_1}}\limits^ \to = \left( {\frac{{100\sqrt 3 }}{3};0; - 100} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 6 (SGK Cánh Diều - Tập 1 - Trang 81)
Trong không gian với hệ tọa độ Oxyz, cho A(– 2; 3; 0), B(4; 0; 5), C(0; 2; – 3).
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.
b) Tính chu vi tam giác ABC.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tính \(\cos\widehat{BAC}\).
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\overrightarrow {AB} = (6; - 3;5),\overrightarrow {AC} = (2; - 1; - 3)\)
\(\overrightarrow {AB} \ne k\overrightarrow {AC} \) nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương hay A, B, C không thẳng hàng
b) Ta có: \(AB = \sqrt {{6^2} + {{( - 3)}^2} + {5^2}} = \sqrt {70} \)
\(AC = \sqrt {{2^2} + {{( - 1)}^2} + {{( - 3)}^2}} = \sqrt {14} \)
\(\overrightarrow {BC} = ( - 4;2; - 8) \Rightarrow BC = \sqrt {{{( - 4)}^2} + {2^2} + {{( - 8)}^2}} = 2\sqrt {21} \)
Chu vi tam giác ABC là: AB + AC + BC = \(\sqrt {70} \)+ \(\sqrt {14} \)+ \(2\sqrt {21} \)
c) Tọa độ trọng tâm G của tam giác ABC là: \(G(\frac{{ - 2 + 4 + 0}}{3};\frac{{3 + 0 + 2}}{3};\frac{{0 + 5 - 3}}{3}) \Rightarrow G(\frac{2}{3};\frac{5}{3};\frac{2}{3})\)
d) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{{6.2 - 3.( - 1) + 5.( - 3)}}{{\sqrt {70} .\sqrt {14} }} = 0\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 2 (SGK Cánh Diều - Tập 1 - Trang 80)
Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow{a}=\left(0;1;1\right)\) và \(\overrightarrow{b}=\left(-1;1;0\right)\). Góc giữa hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) bằng:
A. 60°. B. 120°. C. 150°. D. 30°.
Thảo luận (1)Hướng dẫn giải\(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}} = \frac{{0.( - 1) + 1.1 + 1.0}}{{\sqrt {{0^2} + {1^2} + {1^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {0^2}} }} = \frac{1}{2} \Rightarrow (\overrightarrow a ,\overrightarrow b ) = 60^\circ \)
Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)