Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).
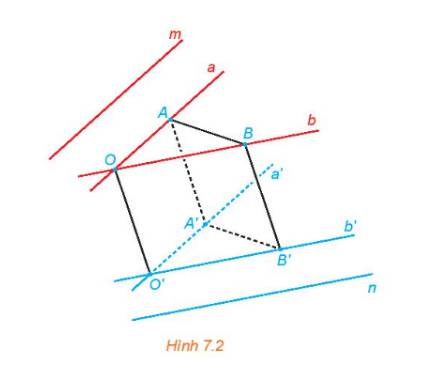
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.
(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').