Cho hai hình bình hành \(ABCD\) và \(ABMN\) không đồng phẳng. Tìm số giao điểm của mặt phẳng \(\left( {ABCD} \right)\) lần lượt với các đường thẳng \(MN,MA\) và \(AC\).
Bài 3. Đường thẳng và mặt phẳng song song
Hoạt động 1 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Thảo luận (1)
Hoạt động 2 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho đường thẳng a không nằm trong mặt phẳng left( P right) và a song song với một đường thẳng b nằm trong left( P right). Đặt left( Q right) mpleft( {a,b} right).a) Tìm giao tuyến của hai mặt phẳng left( P right) và left( Q right).b) Giả sử a có điểm chung M với left( P right) thì điểm M phải nằm trên đường thẳng nào? Điều này có trái với giả thiết aparallel b hay không?
Đọc tiếp
Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\) hay không?
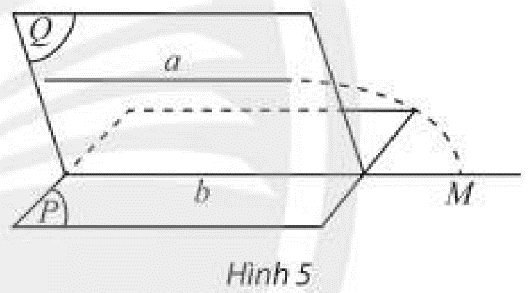
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\left. \begin{array}{l}b \subset \left( P \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow b = \left( P \right) \cap \left( Q \right)\)
Vậy \(b\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}M \in a\\a \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\)
Lại có: \(M \in \left( P \right)\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in b\).
Vậy \(M\) là một điểm chung của hai đường thẳng \(a\) và \(b\), trái với giả thiết \(a\parallel b\).
(Trả lời bởi Quoc Tran Anh Le)
Thực hành 2 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho hình chóp \(S.ABC\) có \(A',B',C'\) lần lượt là trung điểm của \(SA,SB,SC\). Tìm các đường thẳng lần lượt nằm trong, cắt, song song với mặt phẳng \(\left( {ABC} \right)\).
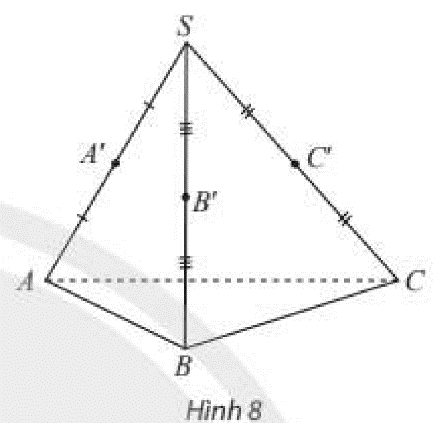
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(B'\) là trung điểm của \(SB\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow B'C'\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)\)
(Trả lời bởi Hà Quang Minh)
Thực hành 3 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Hãy chỉ ra trong Hình 9 các đường thẳng lần lượt nằm trong, song song, cắt mặt phẳng sàn nhà.
Thảo luận (1)Hướng dẫn giảiCác đường thẳng nằm trong mặt phẳng sàn nhà là: mép chân giường, chân tường, mép chân bàn, viền thảm trải sàn,…
Các đường thẳng song song với mặt phẳng sàn nhà là: mép cạnh bàn, mép kệ, mép trần nhà, mép cửa sổ,…
Các đường thẳng cắt mặt phẳng sàn nhà là: cạnh tường, cạnh thẳng đứng của kệ, tủ,…
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Hoạt động 3 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
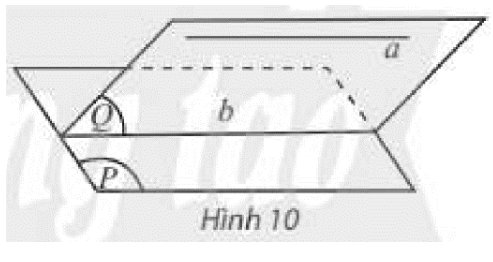
Thảo luận (1)Hướng dẫn giải
Hoạt động 4 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho hai đường thẳng chéo nhau a,b. Lấy một điểm M trên a, vẽ đường thẳng b đi qua M và song song với b. Đặt left( P right) là mặt phẳng đi qua a,b.a) Có nhận xét gì về mối liên hệ giữa b và left( P right).b) Gọi left( {P} right) là mặt phẳng chứa a và song song với b. Có nhận xét gì về mối liên hệ giữa b và left( {P} right); left( P right) và left( {P} right)?
Đọc tiếp
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b'\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b'\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P'} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b'\) và \(\left( {P'} \right)\); \(\left( P \right)\) và \(\left( {P'} \right)\)?
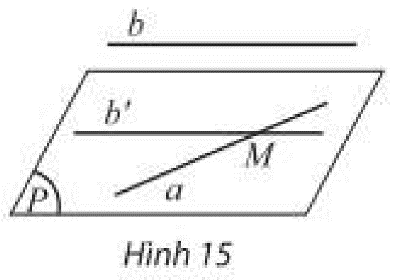
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).
(Trả lời bởi Quoc Tran Anh Le)
Thực hành 3 (Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M,N,E lần lượt là trung điểm của các đoạn thẳng AB,CD,SA (Hình 17). Chứng minh rằng:a) MN song song với hai mặt phẳng left( {SBC} right) và left( {SAD} right);b) SB và SC song song với mặt phẳng left( {MNE} right).
Đọc tiếp
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).
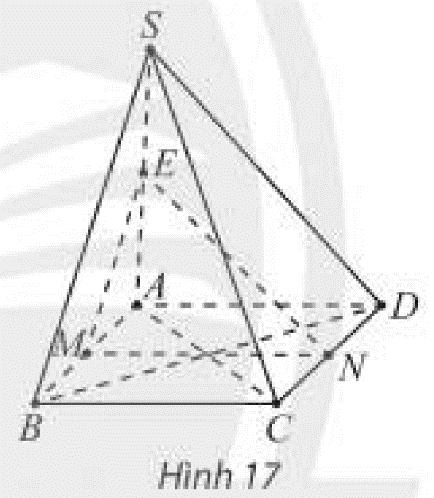
Thảo luận (1)Hướng dẫn giải
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Vận dụng 2 (SGK Chân trời sáng tạo trang 109,110)
Làm thế nào để đặt cây thước kẻ \(a\) để nó song song các trang của một cuốn sách?
Thảo luận (1)Hướng dẫn giảiĐể đặt cây thước kẻ \(a\) song song các trang của một cuốn sách, ta đặt nó song song với mép cuốn sách.
(Trả lời bởi Quoc Tran Anh Le)
Bài 1 (Bài 1 trang 111 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm hai đường chéo. Cho \(M\) là trung điểm của \(SC\).
a) Chứng minh đường thẳng \(OM\) song song với hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBA} \right)\);
b) Tìm giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\).
Thảo luận (1)Hướng dẫn giải
a) \(M\) là trung điểm của \(SC\)
\(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\( \Rightarrow OM\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OM\parallel SA\\SA \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SA{\rm{D}}} \right)\)
Ta có:
\(\left. \begin{array}{l}OM\parallel SA\\SA \subset \left( {SBA} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SBA} \right)\)
b) Ta có:
\(\left. \begin{array}{l}D \in \left( {OM{\rm{D}}} \right) \cap \left( {SA{\rm{D}}} \right)\\OM \subset \left( {OM{\rm{D}}} \right)\\SA \subset \left( {SA{\rm{D}}} \right)\\OM\parallel SA\end{array} \right\}\)
\( \Rightarrow \) Giao tuyến của hai mặt phẳng \(\left( {OMD} \right)\) và \(\left( {SAD} \right)\) là đường thẳng \(d\) đi qua điểm \(D\), song song với \(OM\) và \(SA\).
(Trả lời bởi Quoc Tran Anh Le)
Bài 2 (trang 111 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho hai hình bình hành ABCD và ABEF không nằm trong cùng một mặt phẳng. Gọi O và O lần lượt là tâm của ABCD và ABEF.a) Chứng minh đường thẳng OO song song với các mặt phẳng left( {CDF{rm{E}}} right),left( {ADF} right) và left( {BCE} right).b) Gọi M và N lần lượt là trung điểm của AF và BE. Chứng minh MNparallel left( {CDF{rm{E}}} right).c) Tìm giao tuyến của hai mặt phẳng left( {OMN} right) và left( {ABCD} right).
Đọc tiếp
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
a) Chứng minh đường thẳng \(OO'\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).
b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).
c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).
Thảo luận (1)Hướng dẫn giảiTham khảo hình vẽ:
a) \(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(O'\) là trung điểm của \(BF\) (theo tính chất hình bình hành)
\( \Rightarrow OO'\) là đường trung bình của tam giác \(B{\rm{D}}F\)
\(\left. \begin{array}{l} \Rightarrow OO'\parallel DF\\DF \subset \left( {C{\rm{DFE}}} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {C{\rm{DFE}}} \right)\)
Ta có:
\(\left. \begin{array}{l}OO'\parallel DF\\DF \subset \left( {A{\rm{DF}}} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {A{\rm{DF}}} \right)\)
\(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(O'\) là trung điểm của \(A{\rm{E}}\) (theo tính chất hình bình hành)
\( \Rightarrow OO'\) là đường trung bình của tam giác \(AC{\rm{E}}\)
\(\left. \begin{array}{l} \Rightarrow OO'\parallel CE\\CE \subset \left( {BCE} \right)\end{array} \right\} \Rightarrow OO'\parallel \left( {BC{\rm{E}}} \right)\)
b) \(M\) là trung điểm của \(AF\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(BE\) (theo tính chất hình bình hành)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABEF\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel EF\parallel AB\\EF \subset \left( {C{\rm{D}}F{\rm{E}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {C{\rm{D}}F{\rm{E}}} \right)\)
Ta có:
\(\left. \begin{array}{l}O \in \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN\parallel AB\\MN \subset \left( {OMN} \right)\\AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng \(d\) đi qua \(O\), song song với \(MN\) và \(AB\).
(Trả lời bởi Hà Quang Minh)
