Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\)
Thảo luận (2)Hướng dẫn giảiGọi góc ngoài đỉnh B là x
Ta có:
$\widehat {B} + x = 180^0 $
`=>`$ \widehat {B} + 110^0 = 180^0$
`=>` $\widehat {B} = 70^0$
Xét tứ giác ABCD:
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D}= 360^0$
`=>` $100^0 + 70^0 + 75^0 + \widehat {D} = 360^0$
`=>` $\widehat {D} = 115^0$
Vậy, $\widehat {D} = 115^0.$
(Trả lời bởi 『Kuroba ム Tsuki Ryoo...)
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .

Thảo luận (1)Hướng dẫn giảiXét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
(Trả lời bởi Hà Quang Minh)
Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Thảo luận (1)Hướng dẫn giảia) Trong tứ giác \(ABCD\) có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \\110^\circ + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat B = 360^\circ - \left( {110^\circ + 75^\circ + 75^\circ } \right)\\\widehat B = 100^\circ \end{array}\)
b) Trong tứ giác \(MNPQ\) ta có:
\(\begin{array}{l}\widehat P + \widehat Q + \widehat M + \widehat N = 360^\circ \\90^\circ + 70^\circ + \widehat M + 90^\circ = 360^\circ \\\widehat M = 360^\circ - \left( {90^\circ + 70^\circ + 90^\circ } \right)\\\widehat M = 110^\circ \end{array}\)
c) Ta có: \(\widehat {TSV} = 180^\circ - 60^\circ = 120^\circ \)
Xét tứ giác \(UTSV\) ta có:
\(\begin{array}{l}\widehat U + \widehat T + \widehat S + \widehat V = 360^\circ \\115^\circ + 65^\circ + 120^\circ + \widehat V = 360^\circ \\\widehat V = 360^\circ - \left( {115^\circ + 65^\circ + 120^\circ } \right)\\\widehat V = 60^\circ \end{array}\)
d) Trong tứ giác \(EFGH\) có:
\(\begin{array}{l}\widehat F + \widehat E + \widehat G + \widehat H = 360^\circ \\\widehat F + 80^\circ + 100^\circ + 70^\circ = 360^\circ \\\widehat F = 360^\circ - \left( {80^\circ + 100^\circ + 70^\circ } \right)\\\widehat F = 110^\circ \end{array}\)
(Trả lời bởi Hà Quang Minh)
Tìm \(x\) trong mỗi tứ giác sau:
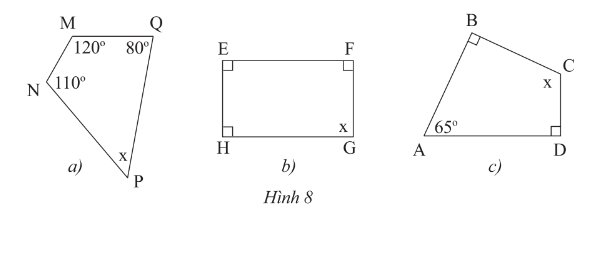
Thảo luận (2)Hướng dẫn giải`a)`
Xét tứ giác `MNPQ:`
$ \widehat {M} + \widehat {N} + \widehat {P} + \widehat {Q} = 360^0$
`=>` $120^0 + 110^0 + \widehat {P} + 80^0 = 360^0$
`=>`$ \widehat {P} = 50^0$
`=>` $x = \widehat {P}= 50^0$
Vậy, `x = 50^0`
`b)`
Xét tứ giác `EFGH:`
$\widehat {E} + \widehat {F} + \widehat {G} + \widehat {H} = 360^0$
`=>` $90^0 + 90^0 + \widehat {G} + 90^0 = 360^0$
`=>`$\widehat {G} = 90^0$
`=>` $x = \widehat {G} = 90^0$
Vậy, ` x= 90^0`
`c)`
Xét tứ giác `ABCD:`
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D} = 360^0$
`=>` $65^0 + 90^0 + \widehat {C} + 90^0 = 360^0$
`=>` $\widehat {C} = 115^0$
`=>` $\widehat {C} = x = 115^0$
Vậy, `x = 115^0.`
(Trả lời bởi 『Kuroba ム Tsuki Ryoo...)
Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên \(CHRL\) (Hình 6)

Thảo luận (1)Hướng dẫn giải
Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của mỗi tứ giác đối với mỗi đường thẳng đã vẽ.
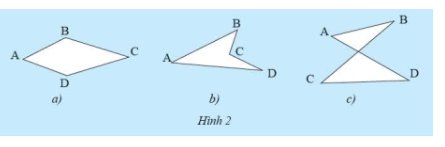
Thảo luận (1)Hướng dẫn giảia: Các cạnh còn lại của tứ giác luôn nằm trong cùg một mặt phẳng
b: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.
c: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Trong các hình tạo bởi bốn đoạn thẳng \(AB\), \(BC\), \(CD\) và \(DA\) sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?
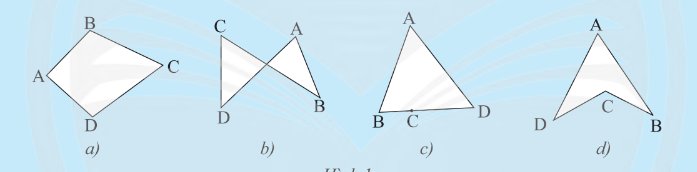
Thảo luận (1)Hướng dẫn giảiHình a,b,d là các hình thỏa mãn yêu cầu
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Vẽ tứ giác \(MNPQ\) và tìm:
- Hai đỉnh đối nhau
- Hai đường chéo
- Hai cạnh đối nhau
Thảo luận (1)Hướng dẫn giải
- Hai đỉnh đối nhau là: \(M\) và \(P\); \(Q\) và \(N\)
- Hai đường chéo là: \(MP\) và \(QN\)
- Hai cạnh đối nhau là: \(MN\) và \(PQ\); \(MQ\) và \(NP\)
(Trả lời bởi Hà Quang Minh)
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Thảo luận (1)Hướng dẫn giảiDo tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(130^\circ + \widehat B + 60^\circ + \widehat D = 360^\circ \)
\(\widehat B + \widehat D = 170^\circ \) (1)
Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AC\) (gt)
\(BC = DC\) (gt)
\(AC\) chung
\( \Rightarrow \Delta ABC = \Delta ADC\) (c-c-c)
\( \Rightarrow \widehat B = \widehat D\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ \)
(Trả lời bởi Hà Quang Minh)