Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).
Bài 2. Tứ giác
Giải bài 4 trang 67 (SGK Toán 8 – Chân trời sáng tạo)
Thảo luận (1)
Giải bài 5 trang 67 (SGK Toán 8 – Chân trời sáng tạo)
Tứ giác \(ABCD\) có số đo \(\widehat A = x;\;\widehat B = 2x;\;\widehat C = 3x;\;\widehat D = 4x\). Tính số đo các góc của tứ giác đó.
Thảo luận (1)Hướng dẫn giảiTrong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên ta có:
\(\begin{array}{l}x + 2x + 3x + 4x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10\\x = 36^\circ \end{array}\)
Suy ra:
\(\widehat A = 36^\circ ;\;\widehat B = 72^\circ ;\;\widehat C = 108^\circ ;\;\widehat D = 144^\circ \)
(Trả lời bởi Hà Quang Minh)
Giải bài 6 trang 67 (SGK Toán 8 – Chân trời sáng tạo)
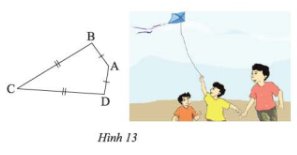
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.
a. Chứng minh rằng AC là đường trung trực của BD.
b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)
(Trả lời bởi Hà Quang Minh)
Giải bài 7 trang 67 (SGK Toán 8 – Chân trời sáng tạo)
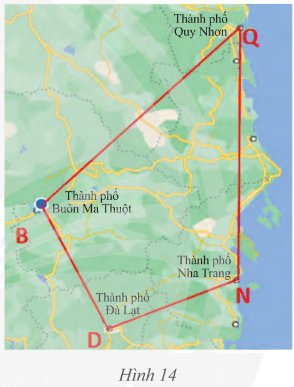
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).
b) Tìm các đường chéo của tứ giác
Thảo luận (1)Hướng dẫn giảia) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)
Cạnh đối của cạnh \(BD\) là: \(NQ\)
b) Các đường chéo của tứ giác là: \(BN;\;DQ\)
(Trả lời bởi Hà Quang Minh)