Tìm điểm giống nhau của các dãy số sau:
a) 2; 5; 8; 11; 14 (xem Hình 1). 
b) 2; 4; 6; 8.
c) 5; 10; 15; 20; 25.
d) ‒5; ‒2; 1; 4; 7; 10.
Bài 2. Cấp số cộng
Hoạt động 1 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Thảo luận (2)
Thực hành 1 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.
a) 3; 7; 11; 15; 19; 23.
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).
c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.
Thảo luận (1)Hướng dẫn giảia) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai \(d = 4\).
b) Ta có: \({u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = 9\).
c) Ta có: \({v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a\).
Vậy dãy số \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = a\).
(Trả lời bởi Quoc Tran Anh Le)
Thực hành 2 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.
Thảo luận (1)Hướng dẫn giảiDo tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.
Đọc tiếp
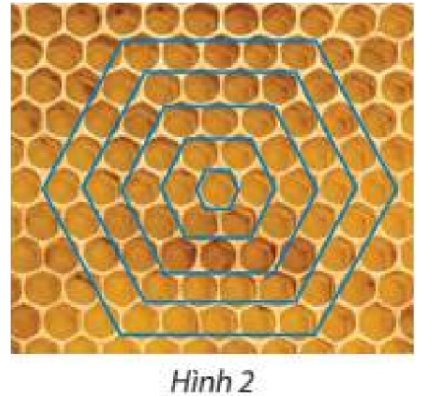
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.
Thảo luận (1)Hướng dẫn giảiDãy số chỉ số ô trên vòng là: \(u_1=6;u_2=12;u_3=18;...\)
Ta thấy: \(u_{n+1}=u_n+6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai d = 6.
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho cấp số cộng \(\left( {{u_n}} \right)\). Hãy cho biết các hiệu số sau đây gấp bao nhiêu lần công sai \(d\) của \(\left( {{u_n}} \right)\): \({u_2} - {u_1};{u_3} - {u_1};{u_4} - {u_1};...;{u_n} - {u_1}\).
Thảo luận (1)Hướng dẫn giải\(u_2-u_1=d\\ u_3-u_1=\left(u_2+d\right)-u_1=\left(u_2-u_1\right)+d=d+d=2d\\ ...\\ u_n-u_1=\left(n-1\right)d\)
(Trả lời bởi Hà Quang Minh)
Thực hành 3 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Tìm số hạng tổng quát của các cấp số cộng sau:
a) Cấp số cộng \(\left( {{a_n}} \right)\) có \({a_1} = 5\) và \(d = - 5\);
b) Cấp số cộng \(\left( {{b_n}} \right)\) có \({b_1} = 2\) và \({b_{10}} = 20\).
Thảo luận (1)Hướng dẫn giảia, Số hạng tổng quát của cấp số cộng \(\left(a_n\right)\) là:
\(a_n=a_1+\left(n-1\right)d=5+\left(n-1\right)\left(-5\right)=5-5n+5=10-5n\)
b, Giả sử cấp số cộng \(\left(b_n\right)\) có công sai d, ta có:
\(b_{10}=b_1+\left(10-1\right)d\\ \Leftrightarrow20=2+9d\\ \Leftrightarrow9d=18\\ \Leftrightarrow d=2\)
Vậy số hạng tổng quát của cấp số cộng \(\left(b_n\right)\) là:
\(b_n=b_1+\left(n-1\right)d=2+\left(n-1\right)\cdot2=2+2n-2=2n\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Tìm số hạng tổng quát của cấp số cộng \(\left( {{c_n}} \right)\) có \({c_4} = 80\) và \({c_6} = 40\).
Thảo luận (1)Hướng dẫn giảiGiả sử cấp số cộng \(\left(c_n\right)\) có số hạng đầu \(c_1\) và công sai d.
Ta có:
\(c_4=c_1+\left(4-1\right)d=c_1+3d\Leftrightarrow c_1+3d=80\left(1\right)\\ c_6=c_1+\left(6-1\right)d=c_1+5d\Leftrightarrow c_1+5d=40\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}c_1+3d=80\\c_1+5d=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c_1=140\\d=-20\end{matrix}\right.\)
Vậy số hạng tổng quát của cấp số cộng \(\left(c_n\right)\) là:
\(c_n=c_1+\left(n-1\right)d=140+\left(n-1\right)\left(-20\right)=160-20\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có công sai \(d\).
a) Tính các tổng: \({u_1} + {u_n};{u_2} + {u_{n - 1}};{u_3} + {u_{n - 2}};...;{u_k} + {u_{n - k + 1}}\) theo \({u_1},n\) và \(d\).
b) Chứng tỏ rằng \(2\left( {{u_1} + {u_2} + ... + {u_n}} \right) = n\left( {{u_1} + {u_n}} \right)\).
Thảo luận (1)Hướng dẫn giải\(a,u_1+u_n=u_1+\left[u_1+\left(n-1\right)d\right]=u_1+u_1+\left(n-1\right)d=2u_1+\left(n-1\right)d\\ u_2+u_{n-1}=\left[u_1+d\right]+\left[u_1+\left(n-2\right)d\right]=2u_1+\left(n-1\right)d\\ ...\\ u_k+u_{n-k+1}=\left[u_1+\left(k-1\right)d\right]+\left[u_1+\left(n-k+1-1\right)d\right]=2u_1+\left(n-1\right)d\)
\(b,u_1+u_n=2u_1+\left(n-1\right)d\\ u_2+u_{n-1}=2u_1+\left(n-1\right)d\\ ...\\ u_n+u_1=2u_1+\left(n-1\right)d\)
Cộng vế với vế, ta được:
\(2\left(u_1+u_2+...+u_n\right)=n\left[2u_1+\left(n-1\right)d\right]\\ \Leftrightarrow2\left(u_1+u_2+...+u_n\right)=n\left(u_1+u_n\right)\)
(Trả lời bởi Hà Quang Minh)
Thực hành 4 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
a) Tính tổng 50 số tự nhiên chẵn đầu tiên.
b) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_3} + {u_{28}} = 100\). Tính tổng 30 số hạng đầu tiên của cấp số cộng đó.
c) Cho cấp số cộng \(\left( {{v_n}} \right)\) có \({S_6} = 18\) và \({S_{10}} = 110\). Tính \({S_{20}}\).
Thảo luận (1)Hướng dẫn giảia, Ta có thể sắp xếp 50 số tự nhiên chẵn đầu tiên thành cấp số cộng có số hạng đầu \(u_1=0\) và công sai \(d=2\)
b, Giả sử cấp số cộng có số hạng đầu \(u_1\) và công sai d.
Ta có:
\(u_3+u_{28}=\left(u_1+2d\right)+\left(u_1+27d\right)=2u_1+29d\Leftrightarrow2u_1+29d=100\\ \Rightarrow S_{30}=\dfrac{30\cdot\left[2u_1+29d\right]}{2}=\dfrac{30\cdot100}{2}=1500\)
c, Giả sử cấp số cộng có số hạng đầu \(v_1\) và công sai \(d\)
Ta có:
\(S_6=18\Leftrightarrow\dfrac{6\cdot\left[2v_1+5d\right]}{2}=18\Leftrightarrow2v_1+5d=6\left(1\right)\\ S_{10}=110\Leftrightarrow\dfrac{10\cdot\left[2v_1+9d\right]}{2}=110\Leftrightarrow2v_1+9d=22\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2v_1+5d=6\\2v_1+9d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_1=-7\\d=4\end{matrix}\right.\)
\(\Rightarrow S_{20}=\dfrac{20\cdot\left[2v_1+19d\right]}{2}=\dfrac{20\cdot\left[2\cdot\left(-7\right)+19\cdot4\right]}{2}=620\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 3 (Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Một rạp hát có 20 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 17 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 23 ghế,… cứ thế tiếp tục cho đến hàng cuối cùng (Hình 4).
a) Tính số ghế có ở hàng cuối cùng.
b) Tính tổng số ghế có trong rạp.
Thảo luận (1)Hướng dẫn giảiTheo đề bài ta có dãy số chỉ số ghế có ở các hàng là một cấp số cộng có số hạng đầu \({u_1} = 17\) và công sai \(d = 3\).
a) Số ghế có ở hàng cuối cùng là: \({u_{20}} = {u_1} + 19{\rm{d}} = 17 + 19.3 = 74\) (ghế).
b) Tổng số ghế có trong rạp là: \({S_{20}} = \frac{{20\left[ {2{u_1} + 19{\rm{d}}} \right]}}{2} = \frac{{20\left[ {2.17 + 19.3} \right]}}{2} = 910\) (ghế).
(Trả lời bởi Quoc Tran Anh Le)