Trong một kì thi học sinh giỏi Toán, tỉ lệ học sinh đạt giải là 35%. Chọn ngẫu nhiên một học sinh đã tham gia kì thi đó. Tính xác suất của biến cố: “Học sinh được chọn đạt giải”.

Những câu hỏi liên quan
Một lớp học có 40 học sinh trong đó có 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
a) Xác suất của biến cố A:”học sinh được chọn giỏi Toán” là:
A. 1/40
B. 8/3
C. 3/8
D. 1/8Ta có n(Ω) = 40
Ta có n(Ω) = 40
a) Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8
Chọn đáp án là C
Đúng 0
Bình luận (0)
Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
b) Xác suất của biến cố B:”học sinh được chọn giỏi Văn” là:
A. 1/40
B. 1/4
C. 4
D. 1/8
Ta có n(Ω) = 40
b) Rõ ràng n(B) = 10 nên P(B) = 10/40 =1/4
Chọn đáp án B
Đúng 0
Bình luận (0)
Đề thi học sinh giỏi: 5 học sinh tham dự kì thi chọn học sinh giỏi Toán đạt được tổng số 69 điểm và trong số 5 người ai cũng đạt được một trong 3 giải: Nhất (15 điểm), nhì (14 điểm) và ba (13 điểm). Hỏi có bao nhiêu trong số 5 học sinh giành được mỗi giải
Giả sử cả 5 người đều được giải ba thì tổng điểm là:
13 x 5 = 65 điểm
Như vậy so với điểm thực tế họ đạt được (69 đ) thì còn thiếu 4 điểm.
Cứ thay 1 giải ba bằng 1 giải nhất thì tổng điểm tăng lên 2;
Cứ thay 1 giải ba bằng 1 giải nhì thì tổng điểm tăng lên 1.
Ta có các trường hợp sau (đều tăng lên 4 đ):
TH1: 4 = 2.2 (tức là 2 bạn đạt giải nhất, 3 bạn còn lại vẫn giữ giải ba)
TH2: 4 = 1.2 + 2.1 (tức là 1 bạn giải nhất, 2 bạn giải nhì, còn 2 bạn còn lại vẫn giữ giải ba)
TH3: 4 = 4.1 (tức là 4 bạn đạt giải nhì và 1 bạn còn lại vẫn giữ giải ba).
ĐS: Có 3 trường hợp:
- TH1: 2 giải nhất, 3 giải ba
- TH2: 1 giải nhất, 2 giải nhì, 2 giải ba
- TH3: 4 giải nhì và 1 giải ba
Đúng 0
Bình luận (0)
Nếu 5 hs đó đều đặt giải nhì thì tổng điểm là 5x14=70 (điểm)nhiều hơn tổng điểm là 1 điểm suy ra ít nhất có 1 hs đạt 13 điểm
Tổng điểm của 4 hs còn lại là 70-13=57(điểm)
Tb mỗi người còn lại được 57:4=14(điểm)=> có 3 trường hợp
Trường hợp 1:4 bạn còn lại đều đặt 14 điểm và thêm 1 bạn 13 điểm
Trường hợp 2:Trong 4 bạn còn lại 2 bạn đạt 14 điểm 1 bạn đạt 13 điểm 1 bạn đạt 15 điểm và thêm 1 bạn 13 điểm
Trường hợp 3:Trong 4 bạn còn lại 2 bạn đạt 15 điểm 2 bạn đạt 13 điểm và thêm 1 bạn 13 điểm
Đúng 0
Bình luận (0)
Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.
c) Xác suất của biến cố C:”học sinh được chọn không giỏi Văn và Toán” là:
A. 15/32
B. 7/8
C. 1/2
D. Một đáp số khác
Ta có n(Ω) = 40
c) Nhận thấy :
![]()
![]()
Mà P(A∪B) = P(A) + P(B) –P(A∩B), A∩B là biến cố:”học sinh được chọn giỏi cả Văn và Toán” nên n(A∩B)=5/40=1/8
![]()
![]()
Chọn đáp án C
Nhận xét:
ở ý a) và b) học sinh có thể nhầm khi quan niệm: chọn 1 học sinh nên n(A) =n(B) =1 ⇒ phương án A; hoặc chọn 1 học sinh trong 5 học sinh giỏi Toán và Văn nên n(A) =n(B) = 5
⇒ P(A) =P(B) =5/40=1/8 (phương án D); hoặc sử dụng nhầm công thức P(A) =(n(Ω))/(n(A))=8/3;P(B)=(n(Ω))/(n(B))=4 (phương án C)
ở ý c), học sinh có thể nhầm khi quan niệm:
![]()
![]()
![]()
Nhưng A ¯ v à B ¯ không phải là hai biến cố độc lập

![]()
Có thể giải ý c) cách khác như sau:
Số học sinh giỏi Văn và Toán gồm: học sinh giỏi Văn, học sinh hioir Toán, học sinh giỏi cả Văn và Toán nên bằng (15 +10) -5 = 20 em. Do đó, số học sinh không giỏi cả Toán và Văn là 40 – 20 = 20 em, nên n(C) = 20
Vì vậy P(C) =(n(C))/(n(Ω))=1/2
Đúng 0
Bình luận (0)
Một đội tuyển tham dự kì thi học sinh giỏi 3 môn Văn, Toán, Ngoại Ngữ do thành phố tổ chức, đạt được 15 giải. Hỏi đội tuyển học sinh giỏi đó có bao nhiêu học sinh? Biết rằng: Học sinh nào cũng có giải; bất kì môn nào cũng có ít nhất 1 học sinh chỉ đạt một giải; bất kì môn nào cũng có ít nhất 1 học sinh đạt giải cả hai môn; có ít nhất 1 học sinh đạt giải cả ba môn; tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần
Đọc tiếp
Một đội tuyển tham dự kì thi học sinh giỏi 3 môn Văn, Toán, Ngoại Ngữ do thành phố tổ chức, đạt được 15 giải. Hỏi đội tuyển học sinh giỏi đó có bao nhiêu học sinh? Biết rằng: Học sinh nào cũng có giải; bất kì môn nào cũng có ít nhất 1 học sinh chỉ đạt một giải; bất kì môn nào cũng có ít nhất 1 học sinh đạt giải cả hai môn; có ít nhất 1 học sinh đạt giải cả ba môn; tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần
Gọi số học sinh đạt giải cả 3 môn là a ( học sinh ). Gọi số học sinh đạt giải cả 2 môn là b ( học sinh ). Gọi số học sinh chỉ đạt giải 1 môn là c ( học sinh ).
Tổng số giải đạt được là: 3 x a + 2 x b + c = 15 giải.
Vì tổng số số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c. Vì bất kì 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ
Do vậy b = 3
Gỉa sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là: 3 x 2 + 2 x 3 + 4 = 16 > 15 ( loại ).
Do đó a < 2, nên a = 1
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12
Nếu b = 3 thì c = 12 - 2 x 3 = ( đúng )
Nếu b = 4 thì c = 12 - 2 x 4 = 4 ( loại vì trái với điều kiện b < c)
Vậy 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải
Đội tuyển đó có số học sinh là: 1 + 3 + 6 = 10 ( bạn)
Đúng 0
Bình luận (0)
Bài giải:
Gọi số học sinh đạt giải cả 3 môn là a (học sinh)
Gọi số học sinh đạt giải cả 2 môn là b (học sinh)
Gọi số học sinh chỉ đạt giải 1 môn là c (học sinh)
Tổng số giải đạt được là:
3 x a + 2 x b + c = 15 (giải).
Vì tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c.
Vì bất kỳ 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ.
Do vậy b= 3.
Giả sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là:
3 x 2 + 2 x 3 + 4 = 16 > 15 (loại). Do đó a < 2, nên a = 1.
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12.
Nếu b = 3 thì c = 12 - 2 x 3 = 6 (đúng).
Nếu b = 4 thì c = 12 - 2 x 4 = 4 (loại vì trái với điều kiện b < c)
Vậy có 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải.
Đội tuyển đó có số học sinh là:
1 + 3 + 6 = 10 (bạn).
Đúng 0
Bình luận (0)
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:A: “Học sinh được chọn là nữ”.B: “Học sinh được chọn học lớp 8”.C: “Học sinh được chọn là nam và không học lớp 7”.
Đọc tiếp
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
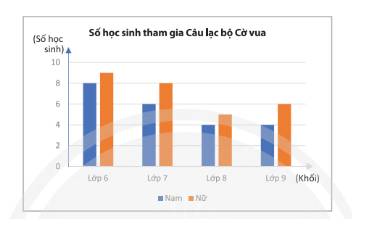
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:
\(A\): “Học sinh được chọn là nữ”.
\(B\): “Học sinh được chọn học lớp 8”.
\(C\): “Học sinh được chọn là nam và không học lớp 7”.
Tổng số học sinh tham gia câu lạc bộ là:
\(8 + 9 + 6 + 8 + 4 + 5 + 4 + 6 = 50\) (học sinh)
- Biến cố \(A\) xảy ra khi bạn học sinh chọn được là nữ.
Số học sinh nữ tham gia câu lạc bộ là:
\(9 + 8 + 5 + 6 = 28\) (học sinh)
Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\)
- Biến cố \(B\) xảy ra khi bạn học sinh chọn được là học sinh lớp 8.
Số học sinh lớp 8 trong câu lạc bộ là:
\(4 + 5 = 9\)(học sinh)
Xác suất của biến có \(B\) là:
\(P\left( B \right) = \frac{9}{{50}}\)
- Biến cố \(C\) xảy ra khi bạn học sinh chọn được là nam và không học lớp 7.
Số học sinh câu lạc bộ là nam và không học lớp 7 là:
\(8 + 6 + 4 = 18\)
Xác suất của biến có \(C\) là:
\(P\left( C \right) = \frac{{18}}{{50}} = \frac{9}{{25}}\)
Đúng 0
Bình luận (0)
1. Một lớp có 100 học sinh trong đó nữ chiếm 70%, còn lại là nam. Tỷ lệ học sinh nữ học giỏi là 40%, tỷ lệ học sinh nam học giỏi là 20%.
a) Chọn ngẫu nhiên một học sinh. Tính xác suất để được học sinh giỏi.
b) Chọn ngẫu nhiên 3 học sinh, tính xác suất có 2 học sinh giỏi.
Lời giải:
a. Xác suất chọn hsg là:
$\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}=\frac{17}{50}$
b.
Chọn ngẫu nhiên 3 hs, có $C^3_{100}$ cách chọn
Số hsg là: $(\frac{40}{100}.\frac{70}{100}+\frac{20}{100}.\frac{30}{100}).100=34$ (hs)
Chọn ngẫu nhiên được 2 hsg có $C^2_{34}C^1_{100-34}=C^2_{34}.C^1_{66}$ cách chọn
Xác suất cần tìm: $p=\frac{C^2_{34}.C^1_{66}}{C^3_{100}}=\frac{561}{2450}$
Đúng 0
Bình luận (0)
Đội tuyển học sinh giỏi Toán 12 trường thpt Yên Dũng số 3 gồm 8 học sinh trong đó có 5 học sinh nam. Chọn ngẫu nhiên 5 học sinh đi thi học sinh giỏi cấp Huyện. Tính xác suất để 5 học sinh được chọn đi thi có cả nam và nữ và học sinh nam nhiều hơn học sinh nữ. A.
p
11
56
B.
p
45
56
C.
p
46
56...
Đọc tiếp
Đội tuyển học sinh giỏi Toán 12 trường thpt Yên Dũng số 3 gồm 8 học sinh trong đó có 5 học sinh nam. Chọn ngẫu nhiên 5 học sinh đi thi học sinh giỏi cấp Huyện. Tính xác suất để 5 học sinh được chọn đi thi có cả nam và nữ và học sinh nam nhiều hơn học sinh nữ.
A. p = 11 56
B. p = 45 56
C. p = 46 56
D. p = 55 56
Đội tuyển học sinh giỏi Toán 12 trường thpt Yên Dũng số 3 gồm 8 học sinh trong đó có 5 học sinh nam. Chọn ngẫu nhiên 5 học sinh đi thi học sinh giỏi cấp Huyện. Tính xác suất để 5 học sinh được chọn đi thi có cả nam và nữ và học sinh nam nhiều hơn học sinh nữ.
Đọc tiếp
Đội tuyển học sinh giỏi Toán 12 trường thpt Yên Dũng số 3 gồm 8 học sinh trong đó có 5 học sinh nam. Chọn ngẫu nhiên 5 học sinh đi thi học sinh giỏi cấp Huyện. Tính xác suất để 5 học sinh được chọn đi thi có cả nam và nữ và học sinh nam nhiều hơn học sinh nữ.
![]()
![]()
![]()
![]()
Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh đi thi. Tìm xác suất để Minh Anh được chọn đi thi. A.
1
7
.
B.
4
7
.
C.
3
7
.
D. ...
Đọc tiếp
Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh đi thi. Tìm xác suất để Minh Anh được chọn đi thi.
A. 1 7 .
B. 4 7 .
C. 3 7 .
D. 1 2 .
Đáp án B
Không gian mẫu n Ω = C 7 4
Gọi biến cố A: “Minh Anh được chọn trong 4 học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có 1 cách.
+ Chọn 3 bạn trong 6 bạn còn lại có C 6 3 cách.
Suy ra n A = 1. C 6 3 = 20.
Vậy xác suất để Minh Anh được chọn đi thi là: P A = n A n Ω = 20 35 = 4 7 .
Đúng 0
Bình luận (0)















