Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm A(2; -2). Giá trị của a bằng
A. 2
B. - 2
C. \(\frac{1}{2}\)
D. \( - \frac{1}{2}\)
2) cho hàm số \(y=\left(a-1\right)x+a\) \(\left(a\ne1\right)\) (1)
a) chứng tỏ: đò thị hàm số (1) luôn đi qua (-1; 1)
b) xác định a để đồ thị (1) cắt trục tung tại điểm có tung độ 3. vẽ đồ thị hàm số
c) xác định a để đò thị (1) cắt trục hoành tại điểm có hoành độ -2. tính khoảng cách từ gốc tọa độ O tới đường thẳng
giúp mk vs ah mk cần gấp
a, gọi điểm hàm số (1) luôn đi qua là A(xo,yo) thì xo,yo thỏa mãn (1)
\(=>yo=\left(a-1\right)xo+a< ->a.\left(xo+1\right)-\left(xo+yo\right)=0\)
\(=>\left\{{}\begin{matrix}xo+1=0\\xo+yo=0\end{matrix}\right.\)=>xo=-1,yo=1 vậy.....
b,\(=>x=0,y=3=>\left(1\right):a=3\)(tm)
c,\(=>x=-2,y=0=>\left(1\right):0=\left(a-1\right)\left(-2\right)+a=>a=2\left(tm\right)\)
\(=>y=x+2\) cho x=0=>y=2=>A(0;2)
cho y=0=>x=-2=>B(-2;0)
gọi OH là khoảng cách từ gốc tọa độ đến đồ thị hàm số(1)
\(=>\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=>\dfrac{1}{OH^2}=\dfrac{1}{2^2}+\dfrac{1}{\left(-2\right)^2}=>OH=....\)
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\) có đường tiệm cận ngang đi qua điểm A (-1;3)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = -2
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
1) Cho hàm số bậc nhất y = (2m -1)x-4 có đồ thị là đường thẳng (d) \(\left(m\ne\dfrac{1}{2}\right)\)
a) Vẽ đồ thị hàm số
b) Tìm tọa độ giao điểm C của (d) với đồ thị hàm số \(y=3x+2\left(d_1\right)\)
2) Tìm m để (d) cắt trục Ox , Oy lần lượt tại A , B sao cho tam giác AOB cân
1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
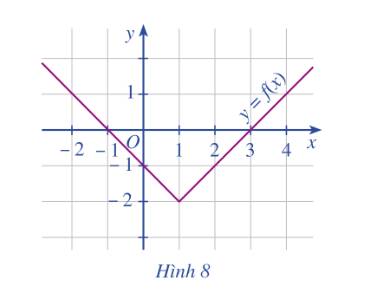
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).
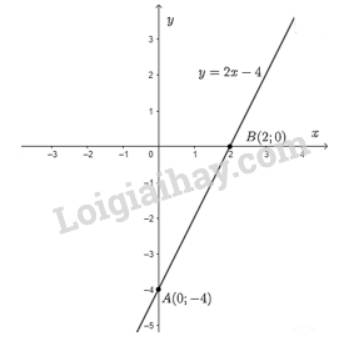
Cho hàm số bậc nhất \(y = ax - 4\)
a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).
b) Vẽ đồ thị của hàm số.
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
Cho hàm số \(y=\left(m-2\right)x+4+m\) . Tìm m để:a) Đồ thị hàm số đi qua điểm A (1 ; 2).b) Đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 4
Để hàm số y=(m-2)x+4+m là hàm số bậc nhất thì \(m-2\ne0\)
hay \(m\ne2\)
a) Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-2)x+4+m, ta được
\(\left(m-2\right)\cdot1+4+m=2\)
\(\Leftrightarrow m-1+4+m=2\)
\(\Leftrightarrow2m+3=2\)
\(\Leftrightarrow2m=-1\)
hay \(m=-\dfrac{1}{2}\)(nhận)
Vậy: Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì \(m=-\dfrac{1}{2}\)
Bài 1: Cho hàm số bậc nhất \(y=ax+b\)
Tìm hệ số a, biết khi \(x=1\)thì \(y=2,5\)
Bài 2: Cho hàm số bậc nhất \(y=ax+b\).Tìm các hệ số a,b biết
a, Đồ thị hàm số cắt trục tung tại điểm có tung độ \(=2\)và đi qua điểm \(A\left(-1,1\right)\)
b, Đồ thị hàm số cắt trục hoành tại điểm có tung độ \(=\left(-2\right)\)và đi qua điểm \(B\left(1;3\right)\)
c, Đồ thị hàm số đi qua 2 điểm \(C\left(2;5\right)\)và \(D\left(-2;-1\right)\)
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\) có đường tiệm cận ngang đi qua điểm M (-2;1)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
Cho hàm số \(y=\left(2a+3\right)x\)
a) Tìm a biết đồ thị hàm số đi qua điểm A(1; -1). Với đồ thị hàm số tìm được, tìm giao điểm của đồ thị đó với đồ thị hàm số \(y=4x-5\)
b) Tìm a biết đồ thị hàm số \(y=\left(2a+3\right)x\)cắt đồ thị hàm số \(y=-2x+2\)tại điểm có hoành độ là 1
a) Vì đồ thị hàm số đi qua A(1;-1) nên ta có :
x= 1 ; y=-1 và thay vào hàm số ta có
y= (2a+3) <=> -1 = (2a + 3)*1 <=> 2a + 3 = -1 <=> 2a = - 3 - 1 <=> 2a = -4 <=> a = -2
Vậy đồ thị hàm số có dạng y = ( -4 +3)x = -1x
- Ta có phương trình hoành độ giao điểm :
-1x = 4x - 5
<=> -1x - 4x = -5
<=>-5x = -5 <=> x = 1 => y = -1x = -1 * 1 = -1
Vậy 2 đồ thị hàm số giao nhau tại B ( 1; -1)
b) Vì hoành độ bằng 1 bằng 1 nên x = 1
Ta có phương trình hoành độ giao điểm :
(2a + 3 )x = -2x +2
thay x = 1 vào phương trình ta có :
( 2a + 3)*1 = -2*1 + 2
<=> 2a + 3 = -2+ 2
<=> 2a = -2 +2 -3 <=> a = \(-\frac{3}{2}\)
Cho hàm số \(y=\left(m+4\right)x+m-1\). Tìm m để hàm số:
a) Có đồ thị đi qua A(2; 9)
b) Có đồ thị đi qua C(-1; -7)
a: Thay x=2 và y=9 vào (d), ta được:
2(m+4)+m-1=9
=>2m+8+m-1=9
=>3m=2
=>m=2/3
b: thay x=-1 và y=-7 vào (d), ta được:
-(m+4)+m-1=-7
=>-m-4+m-1=-7
=>-5=-7(vô lý)