Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat{BEC}\) = 40° và \(\widehat{DFC}\) = 20°, tính số đo các góc của tứ giác ABCD.
Những câu hỏi liên quan
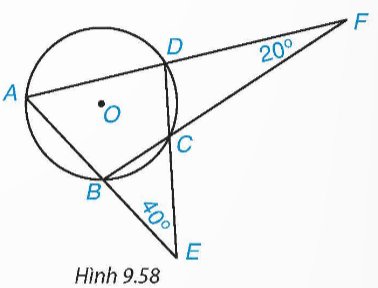
cho tứ giác abcd nội tiếp đường tròn (o), ab cắt cd tại e, ad cắt bc tại f. gọi ex,fy thứ tự là phân giác góc bec và góc dfc. chứng minh ex vuông góc với fy
cho tứ giác ABCD nội tiếp đường tròn tâm O. biết phân giác trong của \(\widehat{BAD}\) và \(\widehat{ABC}\) cắt nhau tại E trên cạnh CD.
1. CM: AD+BC=CD
2. cho \(\dfrac{CD}{CB}=k\) (k>1). tính tỉ số diện tích ΔADE và ΔBCE
Cho tứ giác ABCD biết số đo của các gócwidehat{A}, widehat{B} ,widehat{C}widehat{D} tỉ lệ thuận với 5;8;13 và 10.a) Tính số đo các góc của tứ giác ABCDb) Kéo dài hai cạnh AB và DC cắt nhau ở E,kéo dài hai cạnh AD và BC cắt nhau ở F. Hai tia phân giác của các góc AED và góc AFB cắt nhau ở O.Phân giác của góc AFB cắt các cạnh CD và AB tại M và N.Chứng minh O là trung điểm của đoạn MN
Đọc tiếp
Cho tứ giác ABCD biết số đo của các góc\(\widehat{A}\), \(\widehat{B}\) ,\(\widehat{C}\)\(\widehat{D}\) tỉ lệ thuận với 5;8;13 và 10.
a) Tính số đo các góc của tứ giác ABCD
b) Kéo dài hai cạnh AB và DC cắt nhau ở E,kéo dài hai cạnh AD và BC cắt nhau ở F. Hai tia phân giác của các góc AED và góc AFB cắt nhau ở O.Phân giác của góc AFB cắt các cạnh CD và AB tại M và N.Chứng minh O là trung điểm của đoạn MN
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho điểm O nằm trong tứ giác ABCD và ABCD. AC cắt BD tại E.a) Chứng minh EA.ECEB.EDb) Gọi K trung điểm BC. Đường thẳng qua E và vuông góc OE cắt AD và BC lần lượt tại M,N. Chứng minh tứ giác ENKO nội tiếpc) Chứng minh E trung điểm MNd) Qua D kẻ đường vuông góc với AD. Đường thẳng này cắt đường thẳng vuông góc BC tại C ở F. Chứng minh E,O,F thẳng hàng
Đọc tiếp
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho điểm O nằm trong tứ giác ABCD và AB<CD. AC cắt BD tại E.
a) Chứng minh EA.EC=EB.ED
b) Gọi K trung điểm BC. Đường thẳng qua E và vuông góc OE cắt AD và BC lần lượt tại M,N. Chứng minh tứ giác ENKO nội tiếp
c) Chứng minh E trung điểm MN
d) Qua D kẻ đường vuông góc với AD. Đường thẳng này cắt đường thẳng vuông góc BC tại C ở F. Chứng minh E,O,F thẳng hàng
Cho tứ giác ABCD nội tiếp đường tròn (O). Đường thẳng vuông góc với AD tại A cắt BC
tại E, EO cắt CD tại F. Chứng minh rằng AF vuông góc với AB.
Cho tứ giác ABCD. Đường thẳng DA và BC kéo dài cắt nhau tại E. Đường thẳng AB và CD cắt nhau tại F. Vẽ tia phân giác của \(\widehat{E}\) cắt AB tại M, cắt CD tại K. Vẽ tia phân giác của \(\widehat{F}\) cắt BC tại H, cắt AD tại M.
CMR: Tứ giác MNHK là hình thoi
help me! ( ko cần vẽ hình đâu )
bạn cho đề sai nhé
cắt AD tại N và thứ tự đọc tứ giác là MHKN hoặc ngược lại.
Đúng 0
Bình luận (0)
Cho hình thang ABCD nội tiếp (O) (AD // BC). Các cạnh bên AB,CD cắt nhau tại E. Các tiếp tuyến tại B,D của đường tròn cắt nhau tại F. Chứng minh:
a) Tứ giác BFED nội tiếp đường tròn.
b) EF // BC.
Cho tứ giác ABCD nội tiếp AB cắt CD tại E. Nếu AB=CD=BC(AB>AD) và BEC =200 thì góc ABD= ?
Cho tứ giác ABCD có góc B>90 độ ;góc C> 90 độ ;góc A+góc C= 180 độ .Hai tia AB,DC , cắt nhau tại E và hai tia AD,BC,cắt nhau tại F . Gọi H là giao điểm của các đường phân giác trong của góc BEC và góc DFC . Tính số đo của góc EHF.
16 tháng 3 2023 lúc 17:25
Cho tứ giác ABCD nội tiếp đường tròn (O) có AB = BD. Các đường thẳng AB và DC cắt nhau tại N, đường thẳng CB cắt tiếp tuyến tại A của đường tròn (O) tại M. Chứng minh \(\widehat{AMN}=\widehat{ABD}\)
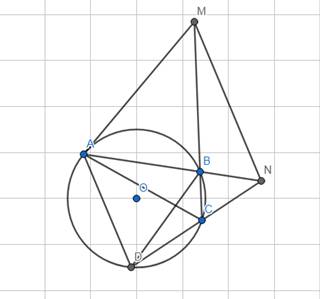
*Chứng minh AMNC là tứ giác nội tiếp.
Ta có AB=BD nên △ABD cân tại B.
\(\Rightarrow\widehat{ADB}=\widehat{BAD}\left(1\right)\)
Trong (O) có: \(\widehat{MAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AB.
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB.
\(\Rightarrow\widehat{MAB}=\widehat{ADB}\left(2\right)\)
Tứ giác ABCD nội tiếp có \(\widehat{BCN}\) là góc ngoài ở đỉnh C.
\(\Rightarrow\widehat{BCN}=\widehat{BAD}\left(3\right)\)
(1), (2), (3) \(\Rightarrow\widehat{MAB}=\widehat{BCN}\).
\(\Rightarrow\)AMNC nội tiếp.
*Chứng minh yêu cầu đề bài.
AMNC nội tiếp \(\Rightarrow\widehat{AMN}=\widehat{ACD}\) (\(\widehat{ACD}\) là góc ngoài ở đỉnh C).
Mà \(\widehat{ACD}=\widehat{ABD}\) (ABCD nội tiếp)
\(\Rightarrow\widehat{AMN}=\widehat{ABD}\) (đpcm)
Đúng 1
Bình luận (0)