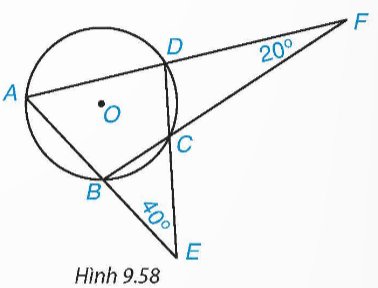
Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat A + \widehat {BCD} = {180^o} \Rightarrow \widehat {BCD} = {180^o} - \widehat A\)
Tam giác ADE có:
\(\widehat {ADC} = {180^o} - \widehat E - \widehat A = {140^o} - \widehat A\)
Tam giác ABF có:
\(\widehat {ABC} = {180^o} - \widehat F - \widehat A = {160^o} - \widehat A\)
Tứ giác ABCD có:
\(\widehat A + \widehat {BCD} + \widehat {ABC} + \widehat {ADC} = {360^o}\)
\( \Rightarrow \widehat A + {180^o} - \widehat A + {140^o} - \widehat A + {160^o} - \widehat A = {360^o}\)
\( \Rightarrow {480^o} - 2\widehat A = {360^o} \Rightarrow \widehat A = {60^o}\)
Do đó, \(\widehat {BCD} = {120^o},\widehat {ADC} = {80^o},\widehat {ABC} = {100^o}\)