(A) Sai. Góc nội tiếp là góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung của đường tròn đó.

(B) Sai. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung hoặc chắn hai cung bằng nhau.

(C) Sai. Trong một đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau.

(D) Sai. Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo của góc ở tâm cùng chắn một cung.

(E) Đúng. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

a , b ,d ,e dung

c sai va dung

a,b,d,e đúng

c sai

Chọn (D) có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.

Phương án (D) đúng :

Góc nội tiếp là góc có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.

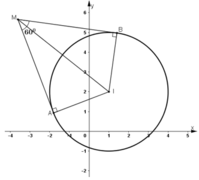
Gọi A, B là hai tiếp điểm của tiếp tuyến kẻ từ M đến (C).

Mà điểm I là cố định nên tập hợp các điểm M là đường tròn tâm I, bán kính R = 6 và có phương trình: (x – 1)2 + (y – 2)2 = 36.

a: góc MAO+góc MBO=180 độ

=>MAOB nội tiếp đường tròn đường kính MO

Tâm là trung điểm của MO

Bán kính là MO/2

b: Xét (O) có

MA,MB là tiếp tuyến

=>MA=MB

mà OA=OB

nên OM là trung trực của AB

=>OM vuông góc AB

góc ABK=1/2*sđ cung AK=90 độ

=>AB vuông góc BK

=>BK//OM

a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)

nên BEFC là tứ giác nội tiếp đường tròn đường kính BC

=>B,E,F,C cùng thuộc một đường tròn

tâm I là trung điểm của BC

b: Xét ΔABC có

BF,CE là các đường cao

BF cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC

=>AM\(\perp\)BC

Xét (O) có

ΔAMD nội tiếp

AD là đường kính

Do đó: ΔAMD vuông tại M

=>AM\(\perp\)MD

Ta có: AM\(\perp\)BC

AM\(\perp\)MD

Do đó: BC//MD

Xét (O) có

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

\(\widehat{ADC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{ABC}=\widehat{ADC}\)

Xét (O) có

ΔACD nội tiếp

AD là đường kính

Do đó: ΔACD vuông tại C

Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(AH\(\perp\)BC)

\(\widehat{ADC}+\widehat{CAD}=90^0\)(ΔACD vuông tại C)

mà \(\widehat{ABC}=\widehat{ADC}\)

nên \(\widehat{BAH}=\widehat{CAD}\)

=>\(\widehat{BAH}+\widehat{MAD}=\widehat{CAD}+\widehat{MAD}\)

=>\(\widehat{BAD}=\widehat{CAM}\)(1)

Xét (O) có

\(\widehat{BAD}\) là góc nội tiếp chắn cung BD

\(\widehat{BCD}\) là góc nội tiếp chắn cung BD

Do đó: \(\widehat{BAD}=\widehat{BCD}\left(2\right)\)

Xét (O) có

\(\widehat{CBM}\) là góc nội tiếp chắn cung CM

\(\widehat{CAM}\) là góc nội tiếp chắn cung CM

Do đó: \(\widehat{CBM}=\widehat{CAM}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\widehat{CBM}=\widehat{BCD}\)

Xét tứ giác BCDM có BC//DM

nên BCDM là hình thang

Hình thang BCDM có \(\widehat{CBM}=\widehat{BCD}\)

nên BCDM là hình thang cân

c: Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

=>BA\(\perp\)BD

mà CH\(\perp\)BA

nên CH//BD

Ta có: CD\(\perp\)CA

BH\(\perp\)AC

Do đó: BH//CD

Xét tứ giác BHCD có

BH//CD
BD//CH

Do đó: BHCD là hình bình hành

=>BC cắt HD tại trung điểm của mỗi đường

mà I là trung điểm của BC

nên I là trung điểm của HD

=>H,I,D thẳng hàng

d: Kẻ tiếp tuyến Ax của (O)

Xét (O) có

\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{xAC}=\widehat{ABC}\)

mà \(\widehat{ABC}=\widehat{AFE}\left(=180^0-\widehat{EFC}\right)\)

nên \(\widehat{xAC}=\widehat{AFE}\)

mà hai góc này là hai góc ở vị trí so le trong

nên EF//Ax

Ta có: Ax//EF

Ax\(\perp\)AD

Do đó: AD\(\perp\)EF tại K

a: góc MAO+góc MBO=180 độ

=>MAOB nội tiếp

b: Xét ΔMAC và ΔMDA có

góc MAC=góc MDA

góc AMC chung

=>ΔMAC đồng dạng với ΔMDA

=>MA/MD=MC/MA

=>MA^2=MD*MC