Cho tam giác ABC vuông tại A (Hình 17).
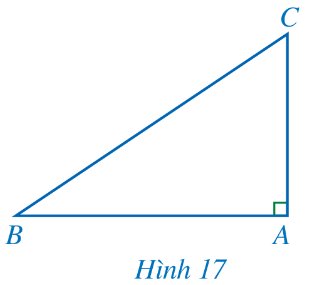
a) Biểu diễn tan B, cot C theo AB, AC.
b) Viết công thức tính AC theo AB và tan B.
c) Viết công thức tính AC theo AB và cot C.
Cho tam giác ABC vuông tại A,AC=5,cot của góc B=2,4.Tính AB,BC.Tính sin,cos,tan,cot của góc C
cho tam giác ABC vuông tại A, đội dài 3 cạnh AB=c,AC=b,BC=a gọi abc = ∝. so sánh a) tan ∝ với sin ∝/ cot ∝ b) cot ∝ với cos ∝ /sin ∝ c) tan ∝ × cot ∝ với 1
b: \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\)
Cho tam giác ABC có \(AB = c, AC = b, \widehat A = \alpha \). Viết công thức tính BC theo \(b,c,\alpha \)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {c^2} + {b^2} - 2.c.b.\cos \alpha \\ \Leftrightarrow BC = \sqrt {{c^2} + {b^2} - 2bc.\cos \alpha } \end{array}\)
Cho △ ABC vuông tại A(AB<AC), có AH là đường cao
1.Biết BC=8cm và \(\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{3}\)
a) tính số đo góc ACB
B) tính độ dài các đoạn thẳng AB,HB,AH
c) tính giá trị của biểu thức cos C-tan B+cot B
2) Gọi E và F lần lượt là h/chiếu của H trên AB,AC,gọi M và N lần lượt là h/chiếu của E và F trên BC.CM\(\sqrt{MB}+\sqrt{NC}=\sqrt{BC}\)
1:
a: Xét ΔABC vuông tại A có \(tanACB=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}}\)
=>\(\widehat{ACB}=30^0\)
b: Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin30=\dfrac{1}{2}\)
=>\(AB=4\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=8^2-4^2=48\)
=>\(AC=4\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot8=4\cdot4\sqrt{3}=16\sqrt{3}\\BH=\dfrac{AB^2}{BC}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{16\sqrt{3}}{8}=2\sqrt{3}\left(cm\right)\\BH=\dfrac{4^2}{8}=2\left(cm\right)\end{matrix}\right.\)
c: \(cosC-tanB+cotB\)
\(=cos30-tan60+cot60\)
\(=\dfrac{\sqrt{3}}{2}-\sqrt{3}+\dfrac{\sqrt{3}}{3}=\dfrac{5}{6}\sqrt{3}-\sqrt{3}=-\dfrac{1}{6}\sqrt{3}\)
Cho tam giác ABC với đường cao BD.
a) Biểu thị BD theo AB và sinA.
b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.
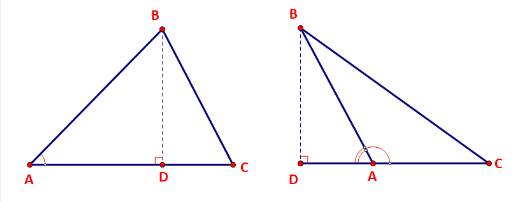
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
TH2: góc A tù
\(\sin A = \sin ({180^o} - A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
Vậy \(BD = AB.\sin A\)
b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)
Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:
\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)
Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)
1) Cho tam giác ABC vuông tại A và đường cao AH, tính AB, AC,HB, HC biết BC=10cm, AH=4cm
2) Cho tan= 1,5. Tính cot, tan, cos
(KO ĐC CHÉP MẠNG)
Câu 2:
\(\cot=\dfrac{2}{3}\)
cho tam giác ABC vuông tại A, đội dài 3 cạnh AB=c,AC=b,BC=a gọi abc = ∝. so sánh
a) tan ∝ với sin ∝/ cot ∝
b) cot ∝ với cos ∝ /sin ∝
c) tan ∝ × cot ∝ với 1
ta có:
. \(\hept{\begin{cases}tan\alpha=\frac{sin\alpha}{cos\alpha}\\cot\alpha=\frac{cos\alpha}{sin\alpha}\\tan\alpha\times cot\alpha=1\end{cases}}\)
Cho tam giác ABC như Hình 10.
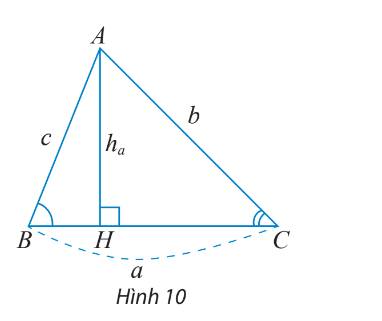
a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)
b) Tính \({h_a}\) theo b và sinC.
c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)
d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)
a) Diện tích S của tam giác ABC là: \(S = \frac{1}{2}a.{h_a}\)
b) Xét tam giác vuông AHC ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b}\)
\( \Rightarrow {h_a} = b.\sin C\)
c) Thay \({h_a} = b.\sin C\) vào công thức diện tích, ta được: \(S = \frac{1}{2}ab\sin C\)
d) Theo định lí sin ta có: \(\frac{c}{{\sin C}} = 2R \Rightarrow \sin C = \frac{c}{{2R}}\)
Thay vào công thức ở c) ta được: \(S = \frac{1}{2}ab\frac{c}{{2R}} = \frac{{abc}}{{4R}}.\)
Cho tam giác ABC vuông tại C, BC = 12cm, AC = 9cm. Tính sin A, cos B, tan A và cot B
Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2+AC^2}=15\left(cm\right)\)
\(sinA=\dfrac{BC}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(cosB=\dfrac{BC}{AB}=\dfrac{4}{5}\)
\(tanA=\dfrac{BC}{AC}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(cotB=\dfrac{BC}{AC}=\dfrac{4}{3}\)
Áp dụng định lí Pytago vào ΔABC vuông tại C, ta được:
\(AB^2=CA^2+CB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Xét ΔABC vuông tại C có
\(\sin\widehat{A}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\cos\widehat{B}=\dfrac{CB}{AB}=\dfrac{12}{15}=\dfrac{4}{5}\)
\(\tan\widehat{A}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{CB}{CA}=\dfrac{12}{9}=\dfrac{4}{3}\)
Tính giùm mình theo công thức từ giữa kì 1đổ lại nha mọi người :
Cho tam giác ABC vuông tại A , AB = 3cm, AC = 4cm.
a) Giải tam giác vuông ABC.(kết quả góc làm tròn đến độ)
b) Kẻ đường cao AH (H∈ BC).Tính độ dài AH và HC.
c) Gọi P và Q lần lượt là hình chiếu của H trên AB, AC. Kẻ QD ⊥ PQ (D ∈ BC).
Tính sinDQH?
b: \(AH=\dfrac{AB\cdot AC}{BC}=2.4\left(cm\right)\)
HC=3,2(cm)