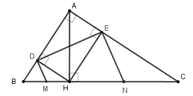
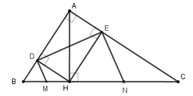
Cho △ ABC vuông tại A(AB<AC), có AH là đường cao
1.Biết BC=8cm và \(\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{3}\)
a) tính số đo góc ACB
B) tính độ dài các đoạn thẳng AB,HB,AH
c) tính giá trị của biểu thức cos C-tan B+cot B
2) Gọi E và F lần lượt là h/chiếu của H trên AB,AC,gọi M và N lần lượt là h/chiếu của E và F trên BC.CM\(\sqrt{MB}+\sqrt{NC}=\sqrt{BC}\)
1:
a: Xét ΔABC vuông tại A có \(tanACB=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}}\)
=>\(\widehat{ACB}=30^0\)
b: Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin30=\dfrac{1}{2}\)
=>\(AB=4\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=8^2-4^2=48\)
=>\(AC=4\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot8=4\cdot4\sqrt{3}=16\sqrt{3}\\BH=\dfrac{AB^2}{BC}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{16\sqrt{3}}{8}=2\sqrt{3}\left(cm\right)\\BH=\dfrac{4^2}{8}=2\left(cm\right)\end{matrix}\right.\)
c: \(cosC-tanB+cotB\)
\(=cos30-tan60+cot60\)
\(=\dfrac{\sqrt{3}}{2}-\sqrt{3}+\dfrac{\sqrt{3}}{3}=\dfrac{5}{6}\sqrt{3}-\sqrt{3}=-\dfrac{1}{6}\sqrt{3}\)