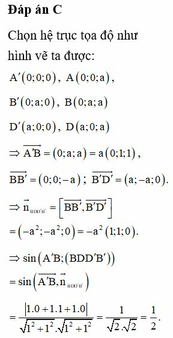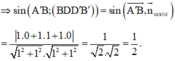Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính \(\overrightarrow{A'B}.\overrightarrow{D'C'};\overrightarrow{D'A}.\overrightarrow{BC}.\)

Những câu hỏi liên quan
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính \(\overrightarrow{BD}.\overrightarrow{D'C}\)
\(\overrightarrow{BD}.\overrightarrow{D'C}=\overrightarrow{BD}\left(\overrightarrow{D'D}+\overrightarrow{DC}\right)=\overrightarrow{BD}.\overrightarrow{D'D}+\overrightarrow{BD}.\overrightarrow{DC}\)
\(=\overrightarrow{BD}.\overrightarrow{DC}=-\overrightarrow{DB}.\overrightarrow{DC}=-a\sqrt{2}.a.cos45^0=-a^2\)
Đúng 1
Bình luận (0)
Cho hình lập phương ABCD.ABCD cạnh a. Gọi O và O theo thứ tự là tâm của hai hình vuông ABCD và ABCD
a) Hãy biểu diễn các vectơ overrightarrow{AO},overrightarrow{AO} theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho
b) Chứng minh rằng :
overrightarrow{AD}+overrightarrow{DC}+overrightarrow{DA}overrightarrow{AB}
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O và O' theo thứ tự là tâm của hai hình vuông ABCD và A'B'C'D'
a) Hãy biểu diễn các vectơ \(\overrightarrow{AO},\overrightarrow{AO'}\) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho
b) Chứng minh rằng :
\(\overrightarrow{AD}+\overrightarrow{D'C}+\overrightarrow{D'A'}=\overrightarrow{AB}\)
Cho hình lập phương ABCD.EFGH có cạnh bằng a . Tính \(\overrightarrow{AB}.\overrightarrow{EG}\) .
bài này ez mà :D ( Tự vẽ hình ) Vì EF // AB nên ta có thể viết như sau:
\(\overrightarrow{AB}.\overrightarrow{EG}=\overrightarrow{EF}.\overrightarrow{EG}=\overrightarrow{EF}\left(\overrightarrow{EF}+\overrightarrow{FG}\right)=EF^2+\overrightarrow{EF}.\overrightarrow{FG}=a^2\)
( Vì: \(\overrightarrow{EF}.\overrightarrow{FG}=\left|\overrightarrow{EF}\right|.\left|\overrightarrow{FG}\right|.\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=0\)) ( \(\cos\left(\overrightarrow{EF},\overrightarrow{FG}\right)=90^0=0\))
Đúng 1
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a . Tính góc giữa 2 đường thẳng A'B và B'D'
\(BD||B'D'\Rightarrow\widehat{\left(A'B;B'D'\right)}=\widehat{\left(A'B;BD\right)}=\widehat{A'BD}\)
Mặt khác \(A'B=BD=A'D=a\sqrt{2}\) (đều là đường chéo của các hình vuông cạnh a)
\(\Rightarrow\Delta A'BD\) đều \(\Rightarrow\widehat{A'BD}=60^0\)
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, gọi
α
là góc giữa đường thẳng
A
B
và mặt phẳng
B
B
D
D
. Tính
sin
α
.
A. ...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α .
A. 3 5 .
B. 3 2 .
C. 1 2 .
D. 3 4 .
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, gọi
α
là góc giữa đường thẳng
A
B
và mặt phẳng
B
B
D
D
. Tính
sin
α
A.
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α
A. 3 5
B. 3 2
C. 1 2
D. 3 4
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Góc giữa hai đường thẳng AB và AC bằng A.
60
°
. B.
30
°
. C.
90
°
. D.
45
°
.
Đọc tiếp
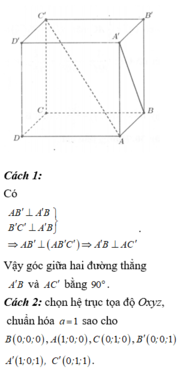
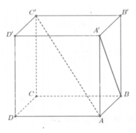
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng A'B và AC' bằng
A. 60 ° .
B. 30 ° .
C. 90 ° .
D. 45 ° .
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Góc giữa hai đường thẳng AB và AC bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
Góc giữa hai đường thẳng A'B và AC' bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.ABCD có cạnh a. Gọi M là trung điểm AB là trung điểm. Tính thể tích của khối tứ diện ADMN A.
V
a
3
3
B.
V
a
3
12
C.
V
a
3
6
D.
V
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi M là trung điểm A'B' là trung điểm. Tính thể tích của khối tứ diện ADMN
A. V = a 3 3
B. V = a 3 12
C. V = a 3 6
D. V = a 3 2
Đáp án C
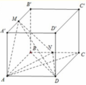
Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:
\(\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD} \)
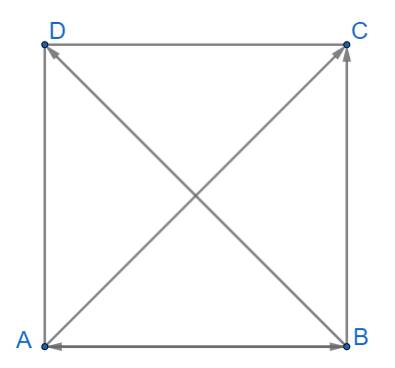
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
Đúng 0
Bình luận (0)