Tìm các khoảng đơn điệu của hàm số
y = x4 + 2x2 – 3.
Xét tính đơn điệu và tìm cực trị của hàm số
y=-x4-2x2+3
\(y'=-4x^3-4x=-4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
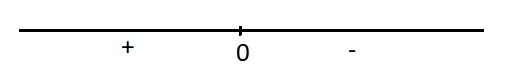
Hàm đồng biến trên \(\left(-\infty;0\right)\) và nghịch biến trên \(\left(0;+\infty\right)\)
Qua \(x=0\) ta thấy y' đổi dấu từ dương sang âm nên \(x=0\) là điểm cực đại
Xét tính đơn điệu của hàm số:
y= x4- 2x2
TXĐ: `D=RR`
`y'=x^3-4x`
`y'=0 <=>` \(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(\begin{array}{|l|cr|} \hline x & -\infty & & -2 &&&& & 0 & &&&&2&&& & +\infty\\ \hline y' & &-& 0& & &+& &0& &&-&&0& &&+&\\ \hline\end{array}\)
Vậy hàm số đồng biến trên các khoảng: `(-2;0)` và `(2; +\infty)`
Hàm số nghịch biến trên các khoảng: `(-\infty; -2)` và `(0;2)`.
Phát biểu các điều kiện đồng biến và nghịch biến của hàm số. Tìm các khoảng đơn điệu của hàm số
y = - x 3 + 2 x 2 - x - 7 ; y = x - 5 1 - x
- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
- Xét hàm số
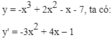
+ Hàm số đồng biến
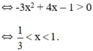
+ Hàm số nghịch biến
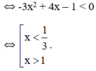
Vậy hàm số đồng biến trên 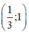
nghịch biến trên các khoảng 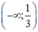 và (1; +∞)
và (1; +∞)
- Xét hàm số 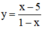
Ta có: D = R \ {1}
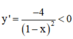 ∀ x ∈ D.
∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).
Cho hàm số y = x4 – 2x2 + 3. Tìm các khoảng đồng biến của hàm số
A. (-∞; -1) và (0; 1)
B. (-1; 0) và (1; +∞)
C. (-∞; 0) và (1; +∞)
D. R
Đáp án A.
TXD: R
Ta có y’ = 4x3 – 4x2 => y’ = 0
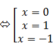
Ta có bảng xét dấu của đạo hàm
Vậy hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Cho các hàm số y = x + 1 x − 1 ; y = x 4 + 2 x 2 + 2 ; y = − x 3 + x 2 − 3 x + 1. Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên ℝ ?
A. 3
B. 1
C. 2
D. 0
Đáp án C.
Ta có
y = − x 3 + x 2 − 3 x + 1 ⇒ y ' = − 3 x 2 + 2 x − 3 < 0 ; ∀ x ∈ ℝ
suy ra hàm số nghịch biến trên ℝ
Tìm khoảng nghịch biến của hàm số sau: y = - x 4 - 2 x 2
A. (-∞; 0)
B. (0; +∞)
C. R
D. (1; +∞)
y = - x 4 - 2 x 2 ⇒ y ' = - 4 x 3 - 4 x = - 4 x ( x 2 + 1 )
y' > 0 ⇔ x < 0; y' < 0 ⇔ x > 0
Do đó, hàm số đã cho nghịch biến trên khoảng .
Chọn B.
Hàm số y = x4 – 2x2 + 3 đồng biến trên các khoảng nào?
A. R
B. (-1 ; 0) và (0 ; 1).
C. (-∞; -1) và (0 ; 1).
D. (-1 ;0) và (1; +∞)
Đáp án D.
y = x4 – 2x2 + 3 => y’ = 4x3 – 4x.
y’ = 0 <=> 4x3 – 4x = 0 <=>![]()
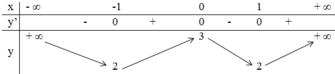
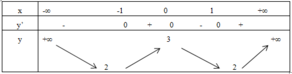
Vậy hàm số đồng biến trên khoảng (-1 ;0) và (1; +∞).
Tìm các khoảng đơn điệu của các hàm số:
y = 2 x x 2 - 9
Tập xác định: D = R \ {±3}
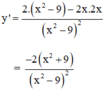
y’ < 0 với ∀ x ∈ D.
y' không xác định tại x = ±3
Bảng biến thiên:
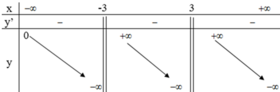
Vậy hàm số nghịch biến trong các khoảng (-∞ ; -3); ( -3; 3) và (3; +∞ ).
Tìm các khoảng đơn điệu của hàm số sau \(y=\dfrac{x+2}{\sqrt{x^2-x+3}}\)
TXĐ: \(D=R\)
\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)
Dấu của y' trên trục số:
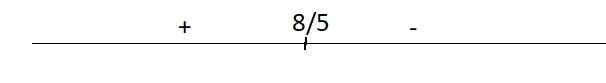
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)
Các khoảng nghịch biến của hàm số y = - x 4 + 2 x 2 - 4 là
A. - ∞ ; - 1 và 1 ; + ∞
B. - 1 ; 0 và 1 ; + ∞
C. - 1 ; 0 và 0 ; 1
D. - ∞ ; - 1 và 0 ; 1