TXĐ: \(D=R\)
\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)
Dấu của y' trên trục số:
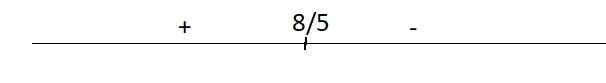
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)
TXĐ: \(D=R\)
\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)
Dấu của y' trên trục số:
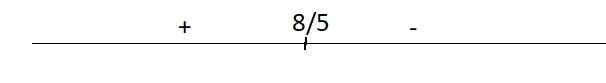
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)
Tìm các khoảng đơn điệu của các hàm số sau:
\(y=x^2+\left|x^2-7x+10\right|\)
Tìm khoảng đơn điệu của các hàm số sau:
a) \(y=\dfrac{3x+1}{1-x}\)
b) \(y=\dfrac{x^2-2x}{1-x}\)
c) \(y=\sqrt{x^2-x-20}\)
d) \(y=\dfrac{2x}{x^2-9}\)
tìm khoảng đơn điệu của hàm số y=|x^2-4x+3|+4x+3
Xét tính đơn điệu của các hàm số :
a) \(y=\sqrt{25-x^2}\)
b) \(y=\dfrac{\sqrt{x}}{x+100}\)
c) \(y=\dfrac{x}{\sqrt{16-x^2}}\)
d) \(y=\dfrac{x^3}{\sqrt{x^2-6}}\)
Cho hàm số \(y=x+3+2\sqrt{2-x}\). Xác định tính đơn điệu của hàm số
Cho các hàm số sau: \(y=\dfrac{1}{3}x^3-x^2+3x+4\); \(y=\sqrt{x^2+4}\);\(y=x^3+4x-sinx\);\(y=x^4+x^2+2\). Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định
xét tính đơn điệu của hàm số y=\(\dfrac{-x^2+2x-1}{x+2}\)
Tìm khoảng đơn điệu của hàm số:
1, \(y=x^2-2\left|x\right|-3\)
2, \(y=sin\left(2x\right)-cos\left(2x\right)+3x\)
Mọi người giúp mình với ạ!! Mình cảm ơn nhiều!!!
Xét tính đơn điệu của hàm số: f(x) = x +\(\sqrt{x^2-4}\)