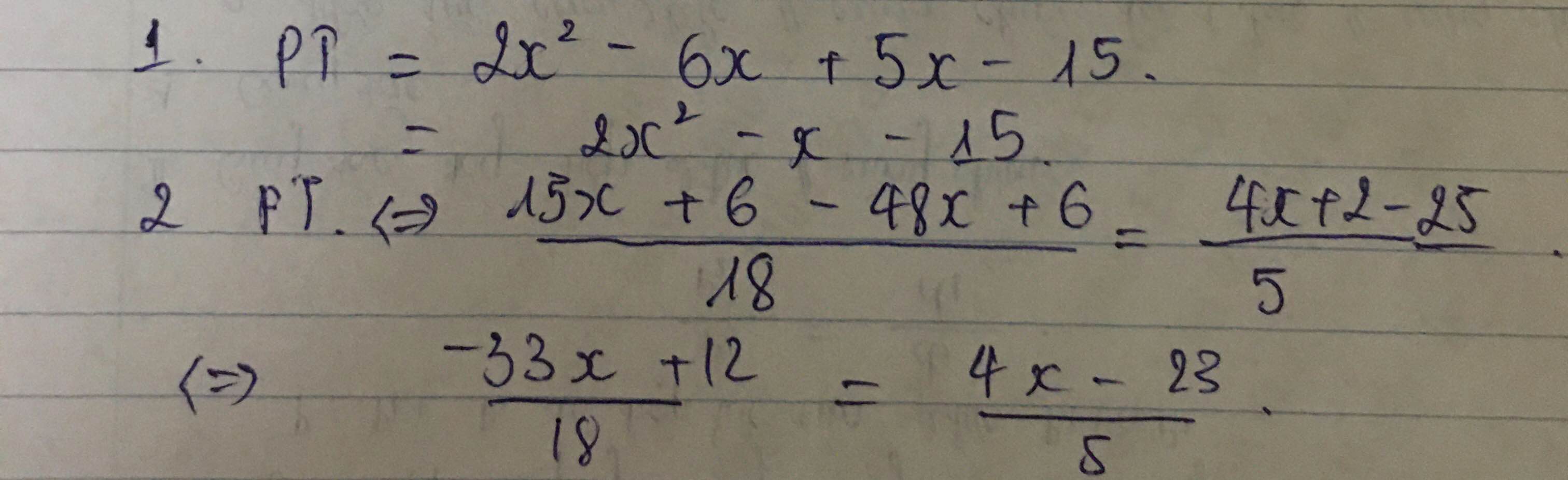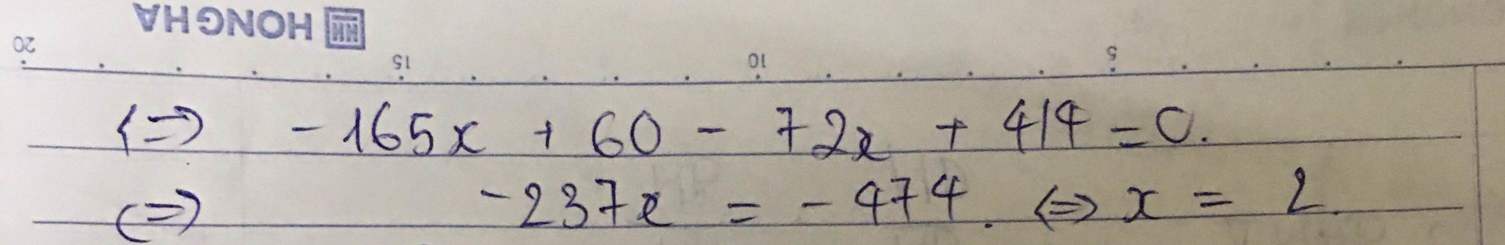Câu 1: 

=>15(2x+1)-8(3x-1)=100

=>30x+15-24x+8=100

=>6x+23=100

hay x=77/6

Câu 2:

=>2(5x-3)+12-3(7x-1)=x+2

=>10x-6+12-21x+3-x-2=0

=>-12x=-7

hay x=7/12

Câu 3: 

\(\Leftrightarrow2\left(x^2-1\right)+3\left(x+1\right)=2\left(x^2-4x+4\right)\)

\(\Leftrightarrow2x^2-2+3x+3-2x^2+8x-8=0\)

=>11x-7=0

hay x=-7/11

Câu 4:

(x - 4)^3/6 + 1 = x(x + 1)/2 - (x - 5)(x + 5)/3

<=> (x - 4)^3 + 6/6 = x^2 + x/2 - x^2 - 25/3

<=> (x - 4)^3 + 6/6 = 3x^2 + 3x - 2x^2 + 50/6

<=> (x - 4)^3 + 6 = 3x^2 + 3x - 2x^2 + 50

<=> x^3 - 12x^2 + 48x - 58 = x^2 + 3x + 50

<=> x^3 -13x^2 + 45x - 108 = 0

Đến đây bạn bấm máy nhẩm nghiệm là ra nhé

Câu 5:

3(x + 2)^3/5 - (x - 1)^2/10 = (x - 3)(x + 3)/2

<=> 6(x + 2)^3 - (x - 1)^2/10 = 5(x^2 - 9)/10

<=> 6(x + 2)^3 - (x - 1)^2 = 5(x^2 - 9)

<=> 6x^3 + 36x^2 + 72x + 48 - x^2 + 2x - 1 - 5x^2 + 45 = 0

<=> 6x^3 + 30x^2 + 74x + 92 = 0

Đến đây bạn bấm máy nhẩm nghiệm như câu 4 nhé

\(1,\) thiếu đề

\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)

\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)

\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)

\(\Leftrightarrow25x+10-80x+10=24x+12-150\)

\(\Leftrightarrow-55x+20=24x-138\)

\(\Leftrightarrow24x-138+55x-20=0\)

\(\Leftrightarrow79x-158=0\)

\(\Leftrightarrow x=2\)

\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)

\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x=0\)

a: =2x^5-15x^3-x^2-2x^5-x^3=-16x^3-x^2

b: =x^3+3x^2-2x-3x^2-9x+6

=x^3-11x+6

c: \(=\dfrac{4x^3+2x^2-6x^2-3x-2x-1+5}{2x+1}\)

\(=2x^2-3x-1+\dfrac{5}{2x+1}\)

a) \(6x^3\left(\dfrac{1}{3}x^2-\dfrac{5}{2}-\dfrac{1}{6}\right)-2x^5-x^3\)

\(=6x^3\left(\dfrac{1}{3}x^2-\dfrac{16}{6}\right)-2x^5-x^3\)

\(=2x^5-16x^3-2x^5-x^3\)

\(=-17x^3\)

b) \(\left(x+3\right)\left(x^2+3x-2\right)\)

\(=x^3+3x^2-2x+3x^2+9x-6\)

\(=x^3+6x^2+7x-6\)

c) \(\left(4x^3-4x^2-5x+4\right):\left(2x+1\right)\)

\(=2x^2+4x^3-2x-4x^2-\dfrac{5}{2}-5x+\dfrac{2}{x}+4\)

\(=4x^3-2x^2-7x+\dfrac{2}{x}+\dfrac{3}{2}\)

a) 1/x(x + 1) + 1/(x + 1)(x + 2) + 1/(x + 2)(x + 3) + 1/(x + 3)(x + 4)

( 1/x - 1/x+1) + (1/x+1 - 1/x+2) + (1/x+2 - 1/ x+3) + 1/(x+3 - 1/x+4)

(1/x +1/x+4) - ( 1/x+2 - 1/x+2) - ( 1/x+3 - 1/x+3)

1/x +1/x+4

2x+4/x(x+4)

Câu b bạn tách các mẫu thành nhân tử rồi làm như câu a nhé

Bài 2:

a: \(=2x^4-x^3-10x^2-2x^3+x^2+10x=2x^3-3x^3-9x^2+10x\)

b: \(=\left(x^2-15x\right)\left(x^2-7x+3\right)\)

\(=x^4-7x^3+3x^2-15x^3+105x^2-45x\)

\(=x^4-22x^3+108x^2-45x\)

c: \(=12x^5-18x^4+30x^3-24x^2\)

d: \(=-3x^6+2.4x^5-1.2x^4+1.8x^2\)

1.

\(\dfrac{2}{3}.\left\{\dfrac{2}{3}-\dfrac{2}{3}.\left[\dfrac{2}{3}-\dfrac{2}{3}.\left(\dfrac{2}{3}-\dfrac{1}{2}\right)\right]\right\}\)

=\(\dfrac{2}{3}.\left\{\dfrac{2}{3}-\dfrac{2}{3}.\left[\dfrac{2}{3}-\dfrac{2}{3}.\dfrac{1}{6}\right]\right\}\)

=\(\dfrac{2}{3}.\left\{\dfrac{2}{3}-\dfrac{2}{3}.\left[\dfrac{2}{3}-\dfrac{1}{9}\right]\right\}\)

=\(\dfrac{2}{3}.\left\{\dfrac{2}{3}-\dfrac{2}{3}.\dfrac{5}{9}\right\}\)

=\(\dfrac{2}{3}.\left\{\dfrac{2}{3}-\dfrac{10}{27}\right\}\)

=\(\dfrac{2}{3}.\dfrac{8}{27}\)

=...

a: \(\left(\sqrt{3}\right)^x=243\)

=>\(3^{\dfrac{1}{2}\cdot x}=3^5\)

=>\(\dfrac{1}{2}\cdot x=5\)

=>x=10

b: \(0,1^x=1000\)

=>\(\left(\dfrac{1}{10}\right)^x=1000\)

=>\(10^{-x}=10^3\)

=>-x=3

=>x=-3

c: \(\left(0,2\right)^{x+3}< \dfrac{1}{5}\)

=>\(\left(0,2\right)^{x+3}< 0,2\)

=>x+3>1

=>x>-2

d: \(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{5}{3}\right)^2\)

=>\(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{3}{5}\right)^{-2}\)

=>2x+1<-2

=>2x<-3

=>\(x< -\dfrac{3}{2}\)

e: \(5^{x-1}+5^{x+2}=3\)

=>\(5^x\cdot\dfrac{1}{5}+5^x\cdot25=3\)

=>\(5^x=\dfrac{3}{25,2}=\dfrac{1}{8,4}=\dfrac{10}{84}=\dfrac{5}{42}\)

=>\(x=log_5\left(\dfrac{5}{42}\right)=1-log_542\)

a: \(=-\dfrac{1}{x\left(x-1\right)}+\dfrac{-1}{\left(x-1\right)\left(x-2\right)}+\dfrac{-1}{\left(x-2\right)\left(x-3\right)}+...+-\dfrac{1}{\left(x-4\right)\left(x-5\right)}+\dfrac{1}{x-5}\)

\(=\dfrac{1}{x}-\dfrac{1}{x-1}+\dfrac{1}{x-1}-\dfrac{1}{x-2}+\dfrac{1}{x-2}-\dfrac{1}{x-3}+...+\dfrac{1}{x-4}-\dfrac{1}{x-5}+\dfrac{1}{x-5}\)

=1/x

b: \(=\dfrac{1}{x}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+6}+\dfrac{1}{x+6}-\dfrac{1}{x+9}+\dfrac{1}{x+9}\)

=1/x

a:

ĐKXĐ: \(x\notin\left\{\dfrac{3}{2};1\right\}\)

 \(y=\dfrac{\left(x-2\right)^2}{\left(2x-3\right)\left(x-1\right)}=\dfrac{x^2-4x+4}{2x^2-2x-3x+3}\)

=>\(y=\dfrac{x^2-4x+4}{2x^2-5x+3}\)

=>\(y'=\dfrac{\left(x^2-4x+4\right)'\left(2x^2-5x+3\right)-\left(x^2-4x+4\right)\left(2x^2-5x+3\right)'}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{\left(2x-4\right)\left(2x^2-5x+3\right)-\left(2x-5\right)\left(x^2-4x+4\right)}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{4x^3-10x^2+6x-8x^2+20x-12-2x^3+8x^2-8x+5x^2-20x+20}{\left(2x^2-5x+3\right)^2}\)

=>\(y'=\dfrac{2x^3-5x^2-2x+8}{\left(2x^2-5x+3\right)^2}\)

b:

ĐKXĐ: x<>-3

 \(y=\left(x+3\right)+\dfrac{4}{x+3}\)

=>\(y'=\left(x+3+\dfrac{4}{x+3}\right)'=1+\left(\dfrac{4}{x+3}\right)'\)

\(=1+\dfrac{4'\left(x+3\right)-4\left(x+3\right)'}{\left(x+3\right)^2}\)

=>\(y'=1+\dfrac{-4}{\left(x+3\right)^2}=\dfrac{\left(x+3\right)^2-4}{\left(x+3\right)^2}\)

y'=0

=>\(\left(x+3\right)^2-4=0\)

=>\(\left(x+3+2\right)\left(x+3-2\right)=0\)

=>(x+5)(x+1)=0

=>x=-5 hoặc x=-1

c:

ĐKXĐ: x<>-2

 \(y=\dfrac{\left(5x-1\right)\left(x+1\right)}{x+2}\)

=>\(y=\dfrac{5x^2+5x-x-1}{x+2}=\dfrac{5x^2+4x-1}{x+2}\)

=>\(y'=\dfrac{\left(5x^2+4x-1\right)'\left(x+2\right)-\left(5x^2+4x-1\right)\left(x+2\right)'}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{\left(5x+4\right)\left(x+2\right)-\left(5x^2+4x-1\right)}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{5x^2+10x+4x+8-5x^2-4x+1}{\left(x+2\right)^2}\)

=>\(y'=\dfrac{10x+9}{\left(x+2\right)^2}\)

\(y'\left(-1\right)=\dfrac{10\cdot\left(-1\right)+9}{\left(-1+2\right)^2}=\dfrac{-1}{1}=-1\)

d: 

ĐKXĐ: x<>2

\(y=x-2+\dfrac{9}{x-2}\)

=>\(y'=\left(x-2+\dfrac{9}{x-2}\right)'=1+\left(\dfrac{9}{x-2}\right)'\)

\(=1+\dfrac{9'\left(x-2\right)-9\left(x-2\right)'}{\left(x-2\right)^2}\)

=>\(y'=1+\dfrac{-9}{\left(x-2\right)^2}=\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}\)

y'=0

=>\(\dfrac{\left(x-2\right)^2-9}{\left(x-2\right)^2}=0\)

=>\(\left(x-2\right)^2-9=0\)

=>(x-2-3)(x-2+3)=0

=>(x-5)(x+1)=0

=>x=5 hoặc x=-1