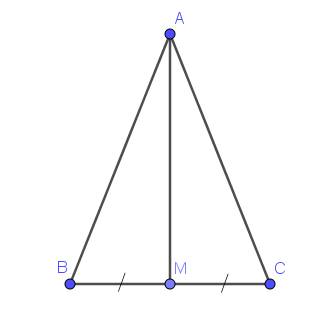
Cho ∆ABC cân tại A. Lấy M là trung điểm của BC. Chứng minh ∆ABC = ∆ACM

Những câu hỏi liên quan
cho tam giác abc cân tại A. Kẻ AH vuông góc BC9 HϵBC, Trên tia AH lấy E sao cho H là trung điểm của AE. Trên tia đối của tia CB lấy điểm F sao cho CF=BC. gọi m là trung điểm của EF
a)chứng minh tam giác abc= ahc
b)chứng minh acm thẳng hàng
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAEF có
FH là đường trung tuyến
FC=2/3FH
Do đó: C là trọng tâm của ΔAEF
=>AC là đường trung tuyến ứng với cạnh FE
mà M là trung điểm của FE
nên A,C,M thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A,M là trung điểm của BC. a) chứng minh: tam giác ABC = tâm giác ACM. b) trên tia đổi của tia MA lấy điểm D sao cho MD=MA. Chứng minh: CD//AB. c) gọi I là trung điểm của AC. Trên tia đổi của tia IB lấy điểm E sao cho IE=IB. Chứng minh: ba điểm D,C,E thẳng hàng và C là trung điểm của DE. Giúp mình
a: Sửa đề: Chứng minh ΔABM=ΔACM
Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔIAB và ΔICE có
IA=IC
\(\widehat{AIB}=\widehat{CIE}\)(hai góc đối đỉnh)
IB=IE
Do đó: ΔIAB=ΔICE
=>\(\widehat{IAB}=\widehat{ICE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
Ta có: AB//CE
AB//CD
CD,CE có điểm chung là C
Do đó: D,C,E thẳng hàng
Ta có: AB=CE(ΔIAB=ΔICE)
AB=CD(ΔIAB=ΔIDC)
Do đó: CE=CD
mà D,C,E thẳng hàng
nên C là trung điểm của DE
Đúng 2
Bình luận (0)
Cho ∆ABC cân tại A , điểm M là trung điểm của cạnh BC . Chứng minh : ∆ABM = ∆ACM , cạnh AMB = AMC
xét △ABM và △ACM có
AB=AC (theo giả thiết)
\(\widehat{B}\) = \(\widehat{C}\) (theo giả thiết)
MB=MC (theo giả thiết)
⇒△ABM=△ACM (c.g.c)
⇒\(\widehat{AMB}\) = \(\widehat{AMC}\) (hai góc tương ứng)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. lấy điểm D thuộc AB, E thuộc AC sao cho AD = AE. Gọi M là trung điểm của BC
a/ Chứng minh tam giác ABM = tam giác ACM
b/ Chứng minh DE song song BC
c/ Chứng minh AM là đường trung trực của BC
Bài 17: Cho tam giác ABC cân tại A. Gọi M là trung điểm BC.
a, Chứng minh \(\Delta\) ABM =\(\Delta\) ACM
b, Chứng minh AM là phân giác góc BAC và AM vuông góc BC.
c, Lấy E bất kì trên đoạn AM. Chứng minh tam giác EBC cân.
Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A có M là trung điểm của cạnh BC. Chứng minh rằng tam giác ABM = tam giác ACM
vì tam giác ABC cân-> AB=AC
do M là trung điểm của BC-> MB=MC
xét tam giác ABM và tam giác ACM có:
AB=AC(cmt)
BM=MC(cmt)
cạnh AM chung
->tam giác ABM=tam giác ACM(c.c.c)
Đúng 1
Bình luận (0)
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (\(\Delta ABC\) cân)
\(\widehat{ABM}=\widehat{ACM}\)(\(\Delta ABC\) cân)
BM = CM (trung điểm M)
\(\Rightarrow\Delta ABM=\Delta ACM\)
Đúng 1
Bình luận (0)
Đây bạn ơi. Thật ra còn nhiều cách nữa nhưng mk mới chỉ liệt kê ra một số cách chi bạn tham khảo thôi

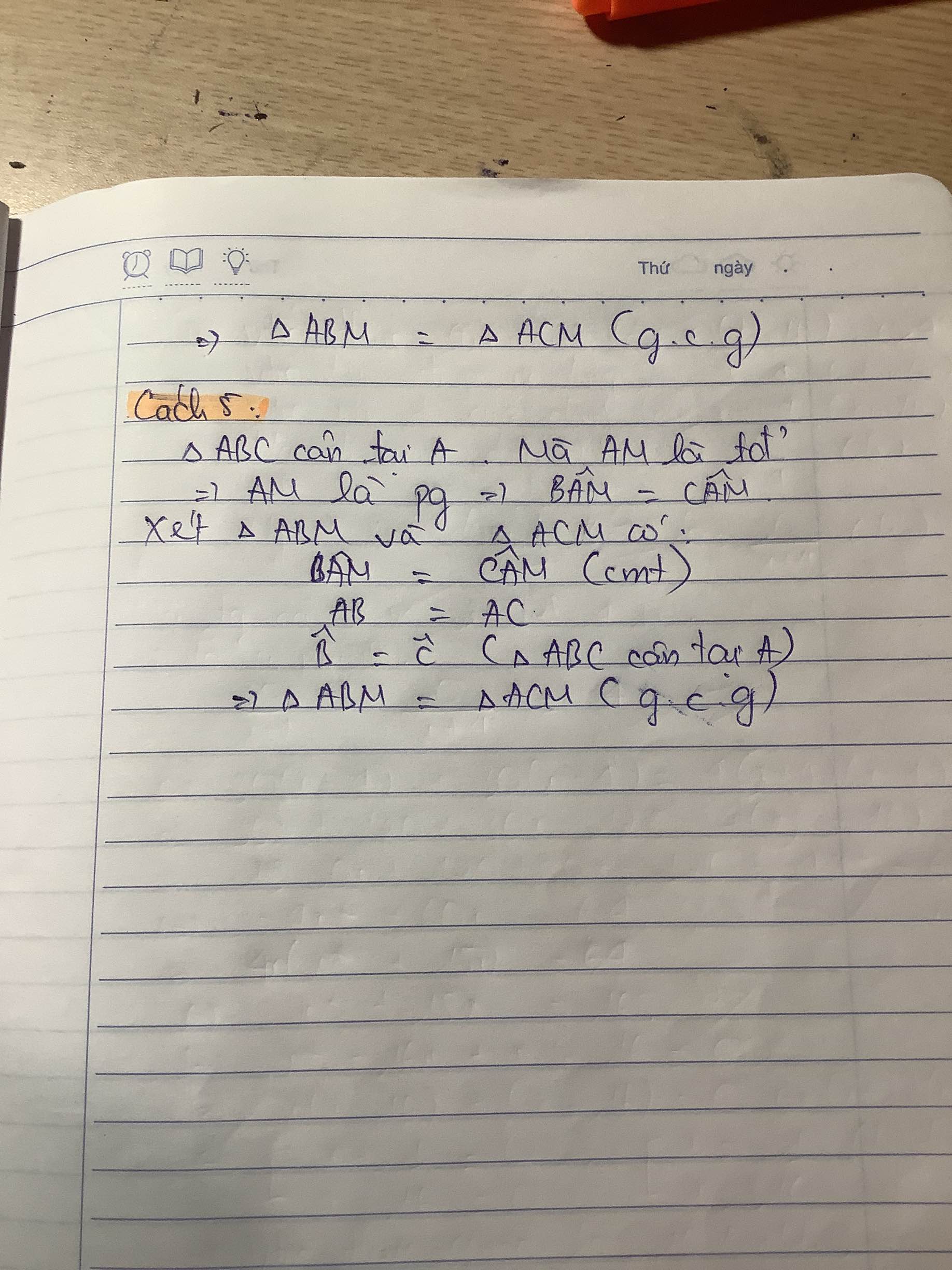
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, M là trung điểm của BC
a) Chứng minh tam giác ABC = tam giác ACM
B) Kẻ MH Vuông góc Ab, MK vuông góc AC
Chứng minh BH = CK , AH= AK
Xem chi tiết
Theo CM câu a ⇒∠B=∠C.
Xét ΔMHB và ΔMKC có:
MB=MC(GT)
∠B=∠C(CM trên)
∠H=∠K=90\(^0\)
Do đó ΔMHB=ΔMKC(CH-GN)
⇒BM=CK(cạnh t.ứng)
Theo cm câu trên ⇒MH=MK
Xét ΔAHM và ΔAKM có
HM=KM(cm trên)
H=K=90\(^O\)(gt)
AM là cạnh chung
Do đó ΔAHM=ΔAKM(c.g.c)
⇒AH=AK(canh t.ứng)
Vậy AH=AK và BH=CK
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc ACB =60°. Trên cạnh BC lấy điểm D sao cho CA=CD. Gọi M là trung điểm của AD:
a, tính góc ABC và chứng tỏ tam giác ACD là tam giác cân
b, Chứng minh: tam giác ACM = tam giác DCM
c, Gọi P là giao điểm của CM và AB. Chứng minh: DP vuông góc BC
a: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+60^0=90^0\)
=>\(\widehat{ABC}=30^0\)
Xét ΔCAD có CA=CD
nên ΔCAD cân tại C
b: Xét ΔCAM và ΔCDM có
CA=CD
AM=DM
CM chung
Do đó: ΔCAM=ΔCDM
c: Ta có: ΔCAM=ΔCDM
=>\(\widehat{ACM}=\widehat{DCM}\)
=>\(\widehat{ACP}=\widehat{DCP}\)
Xét ΔPAC và ΔPDC có
CA=CD
\(\widehat{PCA}=\widehat{PCD}\)
CP chung
Do đó: ΔPAC=ΔPDC
=>\(\widehat{PAC}=\widehat{PDC}\)
mà \(\widehat{PAC}=90^0\)
nên \(\widehat{PDC}=90^0\)
=>PD\(\perp\)BC
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A biết M là trung điểm của bc A, chứng minh tam giác ABM bằng tam giác acm B, trên tia đối của tia ma lấy điểm B sao cho MD = ma chứng minh AC song song với BD C ,vẽ tia Ax song song với BC ( tia Ax và điểm B cùng phía đối với đường thẳng ac đối vs đg thẳng AC)lấy điểm K thuộc tia Ax sao cho AK = B C .Chứng minh ba điểm K B D thẳng
Cho tam giác ABC cân tại A, lấy điểm H là trung điểm của đoạn thẳng BC.
a) chứng minh tam giác ABH = tam giác ACH.
b) tia phân giác của góc ABC cắt đoạn AB tại M, chứng minh góc ABM =góc ACM và tam giác MBC cân.
c) đường thẳng đi qua A và song song với BC cắt tia BM tại N. Chứng minh AB = AN.
d) chứng minh MC vuông góc CN