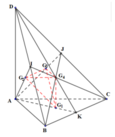
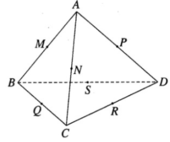
Một tứ diện được gọi là tứ diện trực tâm khi và chỉ khi tứ diện đó có các cặp cạnh đối vuông góc với nhau. (Tứ diện X.YZT là tứ diện trực tâm thì tương đương với \(XY\perp ZT;XT\perp YZ;XZ\perp YT\)). Cho A1A2A3A4 là một tứ diện trực tâm.
a) Hạ \(A_1X_1\perp\left(A_2A_3A_4\right)\) tại X1. Chứng minh rằng X1 là trực tâm của tam giác A2A3A4.
b) Định nghĩa tương tự cho các điểm X2, X3, X4. Chứng minh rằng các đường thẳng \(A_iX_i\left(i=\overline{1,4}\right)\) đồng quy tại một điểm H (H gọi là trực tâm của tứ diện trực tâm A1A2A3A4).
c) Các tứ diện \(HA_iA_jA_k\left(i\ne j\ne k\right)\) có phải là tứ diện trực tâm hay không? Nếu có thì trực tâm của các tứ diện đó là điểm nào?