Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có AB ⊥ CD, AC ⊥ DB, nghĩa là AB → . C D → = 0 và AC → . D B → = 0 thì AD → . B C → = 0 và do đó AD ⊥ BC.”
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì tổng các cặp cạnh đối diện của tứ diện bằng nhau.
Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là: A.
a
7
2
B.
a
6
C.
a
5
6
D....
Đọc tiếp
Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là:
A. a 7 2
B. a 6
C. a 5 6
D. a 15 6
Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc với nhau từng đôi một (như hình vẽ bên dưới). Khẳng địnhnào sau đây sai? A. Góc giữa AD và (ABC) là góc
A
D
B
^
B. Góc giữa CD và (ABD) là góc
C
B
D
^
C. Góc giữa AC và (BCD) là góc...
Đọc tiếp
Cho tứ diện ABCD có các cạnh BA, BC, BD vuông góc
với nhau từng đôi một (như hình vẽ bên dưới). Khẳng định
nào sau đây sai?
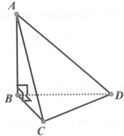
A. Góc giữa AD và (ABC) là góc A D B ^
B. Góc giữa CD và (ABD) là góc C B D ^
C. Góc giữa AC và (BCD) là góc A C B ^
D. Góc giữa AC và (ABD) là góc C A B ^
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OBOCa. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH. A.
a
3
2
6
B.
a
3...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6
Cho hình tứ diện ABCD có DA1, DA vuông góc với (ABC), tam giác ABC đều và có cạnh bằng 1. Trên ba cạnh DA, DB, DC lần lượt lấy M,N,P sao cho
D
M
D
A
1
2
,
3
D
N
D
B
,
4
D
P
3
D
C
.
. Khi đó thể tích khối tứ diện MNPD bằng...
Đọc tiếp
Cho hình tứ diện ABCD có DA=1, DA vuông góc với (ABC), tam giác ABC đều và có cạnh bằng 1. Trên ba cạnh DA, DB, DC lần lượt lấy M,N,P sao cho D M D A = 1 2 , 3 D N = D B , 4 D P = 3 D C . . Khi đó thể tích khối tứ diện MNPD bằng:
A. 3 12 .
B. 2 12 .
C. 3 96 .
D. 2 96 .



