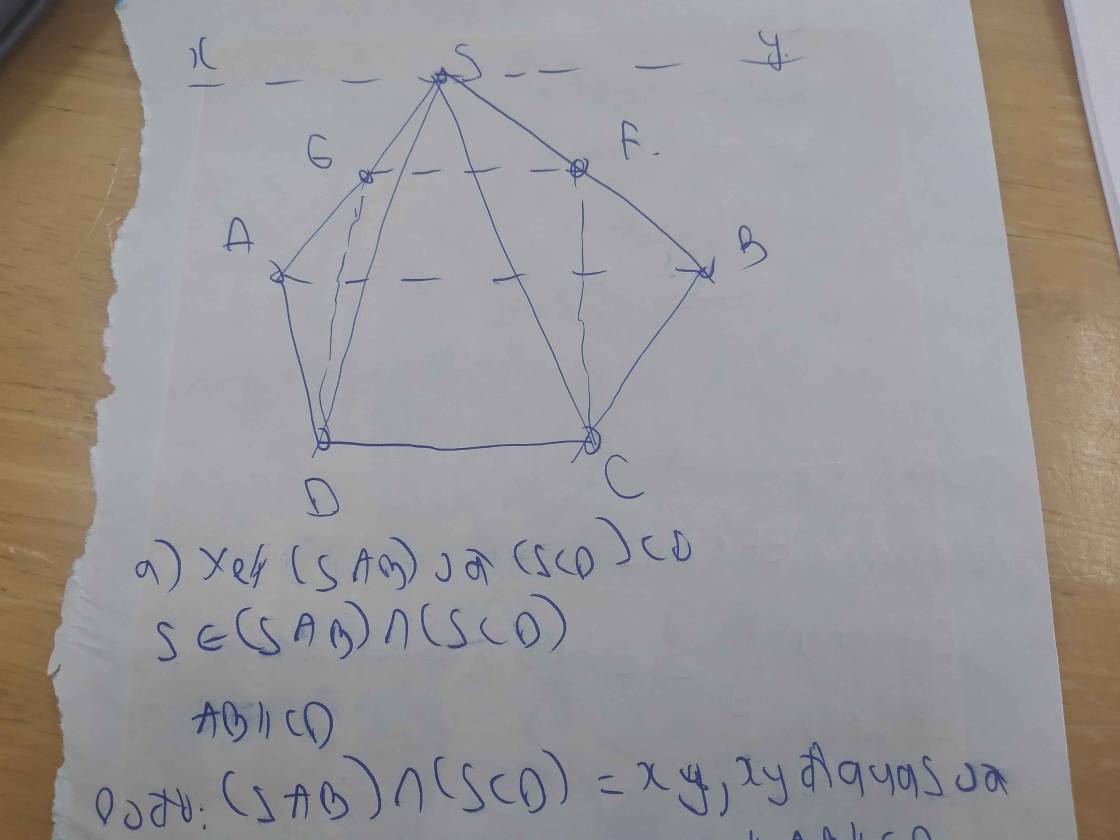
Cho hình chóp s.abcd có ab=2cd. Xác định giao tuyến của (sab) với (scd)

Những câu hỏi liên quan
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD)
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
Tham khảo:

a) Gọi E là giao điểm của AB và CD
Vì AB thuộc mp (SAB) nên E là giao điểm của CD và (SAB)
b) Ta có: S thuộc hai mặt phẳng (SAB) và (SCD)
E thuộc hai mặt phẳng (SAB) và (SCD)
Suy ra SE là giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Trong mp (SAB), gọi G là giao điểm của ME và SB
Mà SB thuộc (SBC), ME thuộc (MCD)
Do đó: G thuộc hai mặt phẳng (MCD) và (SBC)
C thuộc hai mặt phẳng (MCD) và (SBC)
Suy ra CG là giao tuyến của hai mặt phẳng (MCD) và (SBC).
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD và AB < CD. Xác định giao tuyến của hai mặt phẳng sau:
a) (SAD) và (SBC)
b) (SAB) và (SCD)
c) (SAC) và (SBD)
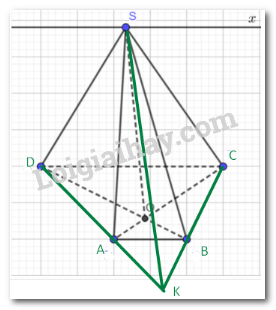
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định giao tuyến của các cặp mặt phẳng (SAB) và (SCD); (SAD) và (SBC).
- Ta có: AB thuộc (SAB)
CD thuộc (SCD)
Mà AB // CD, S là điểm chung của hai mặt phẳng (SAB) và (SCD).
Từ S kẻ Sx sao cho Sx // AB // CD.
Vậy Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
- Tương tự ta có: Sy là giao tuyến của hai mặt phẳng (SAD) và (SBC) sao cho Sy // AD // BC.
Đúng 0
Bình luận (0)
Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB và AB = 2CD. Gọi E, F làn lượt là trung điểm của các cạnh SA, SB. a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD). b) Chứng minh rằng EF // (SCD). c) Chứng minh rằng DE // (SBC). d) Lấy điểm M thuộc cạnh SD. Gọi (P) đi là mặt phẳng qua M và song song với mặt phẳng (SAB). Tim giao tuyến của (P) và (SBC).
Cho hình chóp S.ABCD với ABCD là hình thang đáy lớn AD
a) Xác định giao tuyến của 2 mp (SAB) và (SCD)
b) Gọi M là trung điểm của BC, mp (P) qua M và song song với 2 đường thẳng SA và CD. Xác định thiết diện của mp (P) với hình chóp đã cho
Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp
Đúng 0
Bình luận (0)
1) cho hình chóp S.ABCD đáy ABCD là hình bình hành. Xét vị trí của AB và CD
2) cho hình chóp S.ABCD đáy ABCD là hình vuông
a) xét vị trí của AD và BC
b) tìm giao điểm của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
2:
a: AD và BC là hai đường thẳng song song
b: \(S\in\left(SAB\right)\)
\(S\in\left(SCD\right)\)
Do đó:S là giao điểm của hai mặt phẳng (SAB) và (SCD)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó; \(\left(SAB\right)\cap\left(SCD\right)=mn\), mn đi qua S và mn//AB//CD
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Đáy ABCD là một nửa lục giác đều, 2AB = 2BC = 2CD = AD = 2a, SA=3a. a, Xác định góc giữa (SBD) và (ABCD). b, Xác định góc giữa (SCD) và (SAD).
a: (SBD) giao (ABCD)=BD
SO vuông góc BD
AO vuông góc BD
=>((SBD);(ABCD))=góc SOA
b: (SCD) giao (SAD)=SD
Kẻ AH vuông góc SC
ΔSDC vuông tại D
Kẻ DK vuông góc SC
Qua H kẻ HF//DK
=>Góc cần tìm là góc AHF
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình bình hành.
a) Xác định giao tuyến của (SAB) và (SCD); (SAD) và (SBC).
b) Gọi M\(\in SC\), tìm giao tuyến của (ABM) và (SCD).
c) Gọi N\(\in SB\), tìm giao tuyến của (SAB) và (NCD).
a: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
c: \(N\in SB\subset\left(SAB\right);N\in\left(NCD\right)\)
=>\(N\in\left(SAB\right)\cap\left(NCD\right)\)
Xét (SAB) và (NCD) có
\(N\in\left(SAB\right)\cap\left(NCD\right)\)
AB//CD
Do đó: (SAB) giao (NCD)=ab, ab đi qua N và ab//CD//AB
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là A. Đường thẳng qua S và song song với AD B. Đường thẳng qua S và song song với CD C. Đường SO với O là tâm hình bình hành D. Đường thẳng qua S và cắt AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là
A. Đường thẳng qua S và song song với AD
B. Đường thẳng qua S và song song với CD
C. Đường SO với O là tâm hình bình hành
D. Đường thẳng qua S và cắt AB
Chọn đáp án B
S là điểm chung của hai mặt phẳng (SAB) và (SCD)
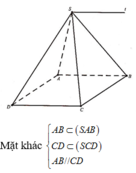
Nên giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng St đi qua điểm S và song song với CD
Đúng 0
Bình luận (0)