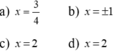\(PT\Leftrightarrow\left|x-3\right|=2x+1\Leftrightarrow\left[{}\begin{matrix}x-3=2x+1\left(x\ge3\right)\\3-x=2x+1\left(x< 3\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-4\left(ktm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{2}{3}\)

\(|x-6|=-5x+9\)

Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)

\(< =>x-6+5x-9=0\)

\(< =>6x-15=0\)

\(< =>x=\frac{15}{6}\)(ktm)

Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)

\(< =>4x-9+6=0\)

\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)

Vậy ...

\(|x+1|=x^2+x\)

Xét \(x\ge-1\)thì \(pt< =>x+1=x^2+x\)

\(< =>x^2+x-x-1=0\)

\(< =>\left(x-1\right)\left(x+1\right)=0\)

\(< =>\orbr{\begin{cases}x=1\\x=-1\end{cases}\left(tm\right)}\)

Xét \(x< -1\)thì \(pt< =>-x-1=x^2+x\)

\(< =>x^2+2x+1=0\)

\(< =>\left(x+1\right)^2=0\)

\(< =>x=-1\left(ktm\right)\)

Vậy ...

Lời giải:

a. Đề thiếu

b. PT $\Leftrightarrow \sqrt{(x-1)^2}+\sqrt{(x-2)^2}=3$

$\Leftrightarrow |x-1|+|x-2|=3$
Nếu $x\geq 2$ thì pt trở thành:
$x-1+x-2=3$

$\Leftrightarrow 2x-3=3$

$\Leftrightarrow x=3$ (tm)

Nếu $1\leq x< 2$ thì:

$x-1+2-x=3\Leftrightarrow 1=3$ (vô lý)

Nếu $x< 1$ thì:

$1-x+2-x=3$

$\Leftrightarrow x=0$ (tm)

x-1 + x-3 =1 <=> 2x -4=1 tu giai not

ĐKXĐ: \(x\ge0\)

\(pt\Leftrightarrow\sqrt{\left(x-3\right)^2}=2x\Leftrightarrow\left|x-3\right|=2x\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=2x\left(x\ge3\right)\\x-3=-2x\left(0\le x< 3\right)\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)

\(\Leftrightarrow\left|x-3\right|=2x\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=2x\left(x\ge3\right)\\x-3=-2x\left(x< 3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)

Lần sao bạn ấn vào Latex để gõ các công thức như thế nào để câu hỏi được rõ hơn nha. Kí hiệu \(\sum\) ở trên thanh công cụ nhé.

Giải:

ĐKXĐ: \(3-2x\ge0\Leftrightarrow3\ge2x\Leftrightarrow x\le\dfrac{3}{2}\)

\(\sqrt{x^2-6x+9}=3-2x\)

\(\Leftrightarrow x^2-6x+9=\left(3-2x\right)^2\\ \Leftrightarrow x^2-6x+9=9-12x+4x^2\\ \Leftrightarrow3x^2-6x=0\\ \Leftrightarrow3x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\)

Vậy x = 0

Lời giải:

a. ĐKXĐ: $x\geq 4$

PT $\Leftrightarrow \sqrt{(x-4)+4\sqrt{x-4}+4}=2$

$\Leftrightarrow \sqrt{(\sqrt{x-4}+2)^2}=2$

$\Leftrightarrow |\sqrt{x-4}+2|=2$

$\Leftrightarrow  \sqrt{x-4}+2=2$

$\Leftrightarrow \sqrt{x-4}=0$

$\Leftrightarrow x=4$ (tm)

b. ĐKXĐ: $x\in\mathbb{R}$

PT $\Leftrightarrow \sqrt{(2x-1)^2}=\sqrt{(x-3)^2}$

$\Leftrightarrow |2x-1|=|x-3|$

\(\Rightarrow \left[\begin{matrix} 2x-1=x-3\\ 2x-1=3-x\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\)

c.

PT \(\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 2x^2-2x+1=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x^2-2x=0\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ 2x(x-1)=0\end{matrix}\right.\Rightarrow x=1\)

ĐK: \(\forall x\in R\)

PT\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{5}{2}\\x^2-6x+9=4x^2-20x+25\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{5}{2}\\3x^2-14x+16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(l\right)\\x=\dfrac{8}{3}\left(tm\right)\end{matrix}\right.\)

Điều kiện :  

\(\left\{{}\begin{matrix}x^2-6x+9\ge0\\2x-5\ge0\end{matrix}\right.\)⇔ \(x\ge\dfrac{5}{2}\)

Ta có : 

\(\left(\sqrt{x^2-6x+9}\right)^2=\left(2x-5\right)^2\)

⇔ \(x^2-6x+9=4x^2-20x+25\)

⇔ \(3x^2-14x+16=0\)

⇔\(\left\{{}\begin{matrix}x=2\left(loại\right)\\x=\dfrac{8}{3}\left(tm\right)\end{matrix}\right.\)

Vì \(VT\ge0\Rightarrow VP\ge0\Rightarrow x\ge\dfrac{5}{2}\)

\(\sqrt{x^2-6x+9}=2x-5\Rightarrow\sqrt{\left(x-3\right)^2}=2x-5\)

\(\Rightarrow\left|x-3\right|=2x-5\)

Xét \(x\ge3\Rightarrow x-3=2x-5\Rightarrow x-2=0\Rightarrow x=2\) (loại)

Xét \(x< 3\Rightarrow\dfrac{5}{2}\le x< 3\Rightarrow3-x=2x-5\Rightarrow3x-8=0\Rightarrow x=\dfrac{8}{3}\) 

Vậy \(x=\dfrac{8}{3}\) là nghiệm của pt...