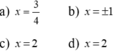Question

Giải các phương trình sau:

a) x − 6 = − 5 x + 9 ;             b) x + 1 = x 2 + x ;  

c) x 2 − 2 x + 4 = 2 x ;             d)  x 2 − x − 6 x − 1 = x − 2 .

Answer 1

Answer 2

\(|x-6|=-5x+9\)

Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)

\(< =>x-6+5x-9=0\)

\(< =>6x-15=0\)

\(< =>x=\frac{15}{6}\)(ktm)

Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)

\(< =>4x-9+6=0\)

\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)

Vậy ...

Answer 3

\(|x+1|=x^2+x\)

Xét \(x\ge-1\)thì \(pt< =>x+1=x^2+x\)

\(< =>x^2+x-x-1=0\)

\(< =>\left(x-1\right)\left(x+1\right)=0\)

\(< =>\orbr{\begin{cases}x=1\\x=-1\end{cases}\left(tm\right)}\)

Xét \(x< -1\)thì \(pt< =>-x-1=x^2+x\)

\(< =>x^2+2x+1=0\)

\(< =>\left(x+1\right)^2=0\)

\(< =>x=-1\left(ktm\right)\)

Vậy ...

Answer 4

\(|x^2-2x|+4=2x\)

\(< =>|x\left(x-2\right)|+4=2x\)

\(< =>|x||x-2|=2x-4\)

Xét \(x< 0\)thì \(pt< =>x\left(x-2\right)=2x-4\)

\(< =>x^2-2x-2x+4=0\)

\(< =>x=2\)(ktm)

Xét \(2>x\ge0\)thì \(pt< =>2x-x^2=2x-4\)

\(< =>x^2-4=0< =>\orbr{\begin{cases}x=2\\x=-2\end{cases}}\left(ktm\right)\)

Xét \(x\ge2\)thì \(pt< =>x\left(x-2\right)=2x-4\)

\(< =>x^2-2x-2x+4=0\)

\(< =>x=2\left(tm\right)\)

Vậy ...