Số nghiệm của phương trình cosx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là
A.5
B.9
C.10
D.11
Những câu hỏi liên quan
Số nghiệm của phương trình sin 3 x 1 - cos x = 0 trên đoạn 0 ; π
A. 4
B. 2
C. 3
D. Vô số
Bài 1 tổng tất cả các nghiệm của phương trình sinx/cosx-1=0 trong đoạn [0;4π]
Bài 2 số vị trí biểu diễn tất cả các nghiệm của phương trình cos2x.tan x=0 trên đường tròn lượng giác là
Cho phương trình
sin
x
1
+
cos
x
0
. Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn
0
;
2018
π
. Tìm số phần tử của tập T A. 2019 B. 1009 C. 1010 D. 2018
Đọc tiếp
Cho phương trình sin x 1 + cos x = 0 . Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn 0 ; 2018 π . Tìm số phần tử của tập T
A. 2019
B. 1009
C. 1010
D. 2018
Cho phương trình
sin
x
1
+
cos
x
0. Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn [0;2018
π
]. Tìm số phần tử của tập T.
Đọc tiếp
Cho phương trình sin x 1 + cos x = 0. Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn [0;2018 π ]. Tìm số phần tử của tập T.
7 tháng 9 2023 lúc 21:25
Phương trình \(\left(2cos2x-\pi\right)\left(sinx-cosx\right)=0\) có số nghiệm thuộc đoạn \(\left[-\pi;\pi\right]\) là
A. 4
B. 5
C. 3
D. 2
=>2cos2x=pi(loại) hoặc sin x-cosx=0
=>sin x-cosx=0
=>sin(x-pi/4)=0
=>x-pi/4=kpi
=>x=kpi+pi/4
mà x\(\in\left[-pi;pi\right]\)
nên \(x\in\left\{\dfrac{pi}{4};-\dfrac{3}{4}pi\right\}\)
=> D
Đúng 0
Bình luận (1)
Số nghiệm của phương trình cos 2 x + cos x - 2 = 0 trong đoạn 0 ; 2 π
A. 2
B. 4
C. 3
D. 1
Số nghiệm của phương trìn sin 3 x 1 - cos x = 0 h trên đoạn [0;ᴨ] là
A. 4
B. 2
C. 3
D. vô số
Số nghiệm của phương trình
cos
2
x
+
cos
x
-
2
0
trong đoạn
0
;
2
π
là: A.2 B.4 C.3 D.1
Đọc tiếp
Số nghiệm của phương trình cos 2 x + cos x - 2 = 0 trong đoạn 0 ; 2 π là:
A.2
B.4
C.3
D.1
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
a) Vẽ đồ thị:
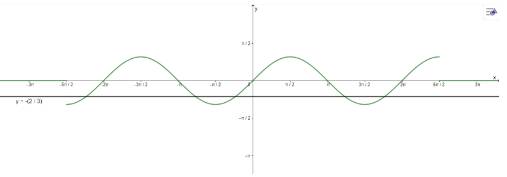
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Đúng 0
Bình luận (0)