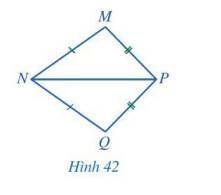
Cho Hình 42 có MN = QN, MP = QP. Chứng minh \(\widehat {MNP} = \widehat {QNP}\).
Cho Hình 66 có \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\). Chứng minh MN = QP, MP = QN.
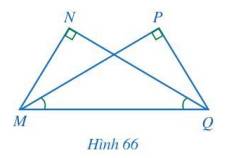
Ta có: tổng ba góc trong một tam giác bằng 180° và \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\) nên \(\widehat {PQM} = \widehat {NMQ}\).
Xét hai tam giác MNQ và QPM có:
\(\widehat {NQM}=\widehat {PMQ}\)
MQ chung
\(\widehat {NMQ}=\widehat {PQM}\)
Vậy \(\Delta MNQ = \Delta QPM\)(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
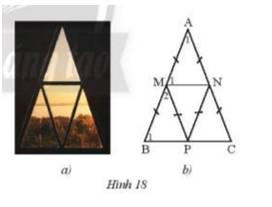
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
Cho tam giác MNP vuông tại M, đường cao MH. Gọi D và E lần lượt là hình chiếu của H trên MN, MP.
a) Tính DE biết MN=15cm, MP=20cm.
b) Chứng Minh \(\widehat{MDE=}\widehat{P}\)
c) Chứng minh MD.MN = MP.ME.
d) Tam giác MNP phải có thêm điều kiện gì để diện tích tứ giác MEHD bằng một nửa diện tích tam giác MNP.
Giải đầy đủ nha!!
Thanks!
Cho △MNP vuông tại M (MN < MP). Kẻ đường phân giác NI của \(\widehat{MNP}\) ( I ∈ MP). Trên cạnh NP lấy điểm K sao cho NK = NM. Chứng minh rằng :
a, △ IMN = △ IKN b, Gọi A là giao điểm KI và NM. Chứng minh NI ⊥ AP
a: Xet ΔIMN và ΔIKN có
NM=NK
góc MNI=góc KNI
NI chung
=>ΔIMN=ΔIKN
=>góc IKN=90 độ
b:Xet ΔNKA vuông tại K và ΔNMP vuông tại M có
NK=NM
góc N chung
=>ΔNKA=ΔNMP
=>NA=NP
=>ΔNAP cân tại N
mà NI là phân giác
nên NI vuông góc PA
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
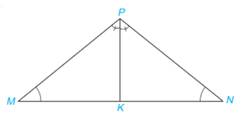
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.
a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm
b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)
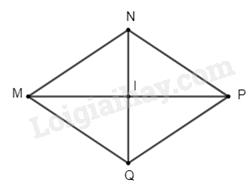
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)
Cho \(\Delta MNP\)có \(\widehat{N}=2\widehat{P}< 90^o\). Vẽ MH vuông góc với NP tại H. Trên tia MN lấy điểm D sao cho MD=HP. Chứng minh đường thẳng DH đi qua trung điểm của đoạn thẳng MP
Cho tam giác MNP vuông tại M có MN=5cm, MP=12cm và đường cao MH.
a. Chứng minh: tam giác MNP đồng dạng tam giác HNM. Từ đó suy ra MN^2=NH.NP
b. Tính NP,NH.
c. Cho NQ là phân giác của góc MNP (Q thuộc MP). Chứng minh: QM/QP và QM,QP.
d. Gọi E là giao điểm MH và NQ. Tính tỉ số S^MNQ/S^HNE
a: Xét ΔMNP vuông tại M và ΔHNM vuông tại H có
góc N chung
DO đó: ΔMNP∼ΔHNM
Suy ra: NM/NH=NP/NM
hay \(NM^2=NH\cdot NP\)
b: NP=13cm
\(NH=\dfrac{MN^2}{NP}=\dfrac{25}{13}\left(cm\right)\)
Mình đang cần gấp!!
Cho tam giác MNP vuông tại M. Kẻ tia phân giác của góc N cắt MP tại D. Trên cạnh NP lấy điểm E sao cho NE = NM
a) Chứng minh: Tam giác NMD = Tam giác NED và \(\widehat{NMD}=\widehat{NED}\)
b) Kẻ EH vuông góc với MP (H thuộc MP). Chứng minh NM // EH
c) So sánh \(\widehat{HEP}=\widehat{MNP}\)
a)
Xét tam giác NMD và tam giác NED, có:
NM=EH(gt)
\(\widehat{MND}=\widehat{DNE}\)(do MD là phân giác MNE)
ND là cạnh chung
Suy ra: Tam giác NMD=tam giác NED (c.g.c)
==> \(\widehat{NMD}=\widehat{NED}\) (2 góc tương ứng)
b) Có: +) MN vuông góc MP
+) EH vuông góc MP
==> MN // EH
c) Có : MN // EH
==> MNP = HEP (2 góc đồng vị)