Question

Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.

a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm

b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)

Answer 1

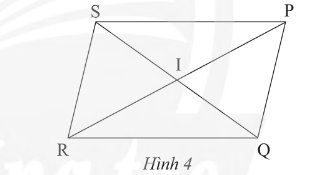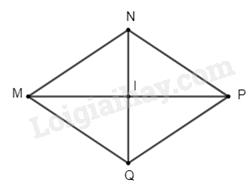
a) Vì \(MNPQ\) là hình thoi (gt)

Suy ra \(IM = IP\) và \(NQ \bot MP\)

Suy ra \(\widehat {{\rm{MIN}}} = 90\)

Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:

\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)

Suy ra \(MI = 8\) (dm)

b) Vì \(MNPQ\) là hình thoi (gt)

Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)

Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)

Xét \(\Delta MNI\) vuông tại \(I\) ta có:

\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)

Suy ra \(\widehat {IMN} = 90^\circ  - \widehat {MNI} = 90^\circ  - 64^\circ  = 26^\circ \)