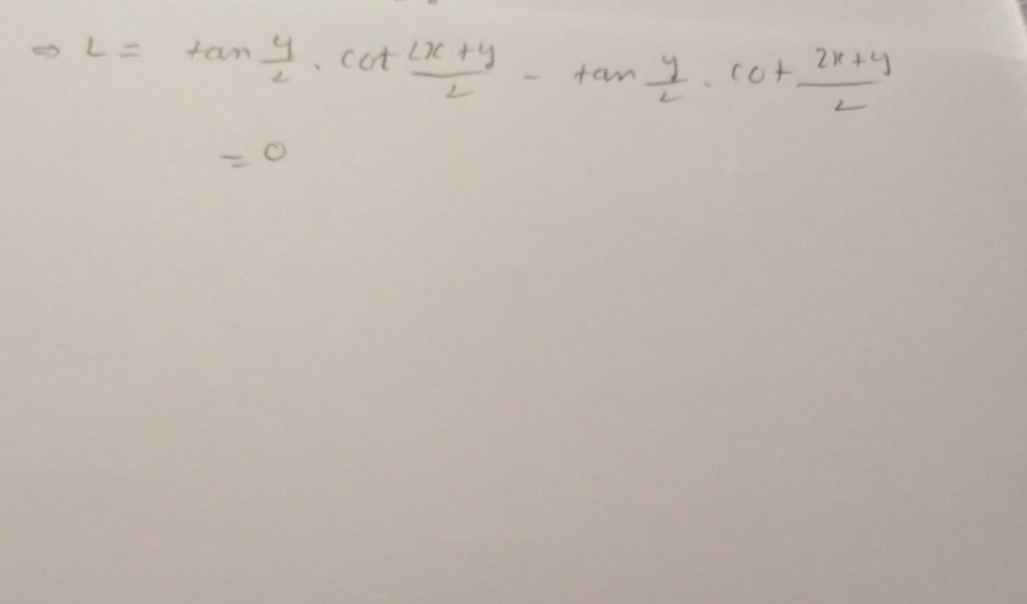đáp án không giống lắm 

2: \(\left(sinx+cosx\right)^2=1+2\cdot sinx\cdot cosx=1+2\cdot\dfrac{\sqrt{3}}{4}=1+\dfrac{\sqrt{3}}{2}=\dfrac{2+\sqrt{3}}{2}\)

=>\(sinx+cosx=\dfrac{\sqrt{3}+1}{2}\)

mà sin x*cosx=căn 3/4

nên sinx,cosx là các nghiệm của phương trình là:

\(a^2-\dfrac{\sqrt{3}+1}{2}\cdot a+\dfrac{\sqrt{3}}{4}=0\)

=>\(\left[{}\begin{matrix}a=\dfrac{\sqrt{3}}{2}\\a=\dfrac{1}{2}\end{matrix}\right.\)

Ta sẽ có hai trường hợp:

TH1: sin x=căn 3/2; cosx=1/2

tan x=sinx/cosx=căn 3

cot x=1/căn 3

TH2: sin x=1/2; cosx=căn 3/2

tan x=sin x/cosx=1/căn 3

cot x=1:1/căn 3=căn 3

Đây nè bn:

1.

\(sin^2x+cos^2x=1\Rightarrow\left(\dfrac{1}{4}\right)^2+cos^2x=1\)

\(\Rightarrow cos^2x=\dfrac{15}{16}\Rightarrow cosx=\dfrac{\sqrt{15}}{4}\)

2.

\(tanx=\dfrac{1}{3}\Rightarrow tan^2x=\dfrac{1}{9}\Rightarrow\dfrac{sin^2x}{cos^2x}=\dfrac{1}{9}\)

\(\Rightarrow\dfrac{sin^2x}{1-sin^2x}=\dfrac{1}{9}\Rightarrow9sin^2x=1-sin^2x\)

\(\Rightarrow sin^2x=\dfrac{1}{10}\Rightarrow sinx=\dfrac{\sqrt{10}}{10}\)

sin x+cosx=m

=>(sinx+cosx)^2=m^2

=>1+2*cosx*sinx=m^2

=>2*sinx*cosx=m^2-1

=>\(sinx\cdot cosx=\dfrac{m^2-1}{2}\)

\(sin^3x+cos^3x=\left(sinx+cosx\right)^3-3\cdot sinx\cdot cosx\cdot\left(sinx+cosx\right)\)\(=m^3-3\cdot\dfrac{m^2-1}{2}\cdot m\)

\(=m^3-\dfrac{3m^3-3m}{2}\)

\(=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{-m^3+3m}{2}\)

Lời giải:

$A=\frac{2\cos \frac{2x+y}{2}\sin \frac{x}{2}}{2\sin \frac{2x+y}{2}.\cos \frac{x}{2}}-\frac{2\cos \frac{2x+y}{2}\cos \frac{x}{2}}{-2\sin \frac{2x+y}{2}\sin \frac{x}{2}}$

$=\tan \frac{x}{2}.\cot \frac{2x+y}{2}+\cot \frac{x}{2}.\cot \frac{2x+y}{2}=\cot \frac{2x+y}{2}(\tan \frac{x}{2}+\cot \frac{x}{2})$