Tìm nghiệm nguyên của phương trình để phương trình là số chính phương
x4+x3+x2+x+1
Những câu hỏi liên quan
Tổng số giá trị nguyên của m để phương trình x 3 + x ( x + 1 ) = m ( x 2 + 1 ) 2 có nghiệm thực là
A. 5
B. 4
C. 7
D. 0
Cho phương trình
x
3
-
3
x
2
+
m
x
-
2
m
+
2
0
(m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 t...
Đọc tiếp
Cho phương trình x 3 - 3 x 2 + m x - 2 m + 2 = 0 (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x1<1<x2<x3?
A.0
B.3
C.5
D.Vô số
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.
Đúng 0
Bình luận (0)
Số giá trị nguyên của tham số m thuộc đoạn
[
-
2019
;
2019
]
để phương trình
x
2
+
(
m
+
2
)
x
+
4
(
m
-
1
)
x
3
+
4
x
có nghiệm là A. 2011. B. 2012. C. 2013. D. 2014.
Đọc tiếp
Số giá trị nguyên của tham số m thuộc đoạn [ - 2019 ; 2019 ] để phương trình x 2 + ( m + 2 ) x + 4 = ( m - 1 ) x 3 + 4 x có nghiệm là
A. 2011.
B. 2012.
C. 2013.
D. 2014.
1/ số nghiệm của phương trình ( x - 1 ) ( x + 7 ) ( x - 5 ) 0 làA. 0B. 1C. 2D. 32/ số nghiệm của phương trình ( x2 - 1 ) ( x2 + 7 ) ( x2 - 4 ) 0 làA. 1B. 2C. 3D. 43/ số nghiệm của phương trình ( x3 - 1 ) ( x2 + 9 ) ( x2 + x + 1 ) 0 LÀ A. 1B.2C.3D.44/ số nghiệm của phương trình ( x3 - 8 ) ( x2 + 9 ) ( x2 - x + 1 ) 0 làA. 1B. 2C. 3D. 4
Đọc tiếp
1/ số nghiệm của phương trình ( x - 1 ) ( x + 7 ) ( x - 5 ) = 0 là
A. 0
B. 1
C. 2
D. 3
2/ số nghiệm của phương trình ( x2 - 1 ) ( x2 + 7 ) ( x2 - 4 ) = 0 là
A. 1
B. 2
C. 3
D. 4
3/ số nghiệm của phương trình ( x3 - 1 ) ( x2 + 9 ) ( x2 + x + 1 ) = 0 LÀ
A. 1
B.2
C.3
D.4
4/ số nghiệm của phương trình ( x3 - 8 ) ( x2 + 9 ) ( x2 - x + 1 ) = 0 là
A. 1
B. 2
C. 3
D. 4
Cho phương trình (2m−5)x2 −2(m−1)x+3=0 (1); với m là tham số thực
1) Tìm m để phương trình (1) có một nghiệm bằng 2, tìm nghiệm còn lại.
3) Tìm giá trị của m để phương trình đã cho có nghiệm
4) Xác định các giá trị nguyên của để phương trình đã cho có hai nghiệm phân biệt đều nguyên dương
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
Đúng 1
Bình luận (0)
cho pt: \(x^3-x^2+2mx-2m=0\left(1\right)\)
a, Tìm m để phương trình có ba nghiệm phân biệt x1,x2,x3 tm: x1+x2+x3=10
b,Tìm m để phương trình có ba nghiệm phân biệt đều lớn hơn hoặc bằng 1.
\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài
Đúng 2
Bình luận (0)
1) Tìm nghiệm nguyên của phương trình : x2= 2y2+2013
2) Giải phương trình x3+2x2- 4x +\(\dfrac{8}{3}\)=0
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
Đúng 0
Bình luận (0)
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
Đúng 0
Bình luận (0)
Cho phương trình
x
3
−
3
x
2
+
1
−
m
0
1
.
Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn
x
1
1
x
2
x
3
là A.
m
−...
Đọc tiếp
Cho phương trình x 3 − 3 x 2 + 1 − m = 0 1 . Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 là
A. m = − 1
B. − 1 < m < 3
C. − 3 < m < − 1
D. − 3 ≤ m ≤ − 1
Đáp án C
Vẽ đồ thị hàm số y = x 3 − 3 x 2 + 1
Để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 thì đường thẳng y=m cắt đồ thị hàm số y = x 3 − 3 x 2 + 1 tại ba điểm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 ⇔ − 3 < m < − 1.
Đúng 0
Bình luận (0)
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
64
|
x
|
3
(
x
2
+
1
)
2
(
12
|
x
|
+
m
(
x
2
+
1
)
)...
Đọc tiếp
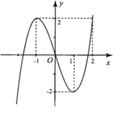
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
A.
B. Với mọi m
C. 
D. 
Đáp án A
(*)
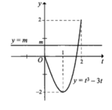
Đặt 
Yêu cầu bài toán trở thành: Tìm m để phương trình 
có nghiệm 
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số 
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán 
Đúng 0
Bình luận (0)