Cho ▲ABC vuông cân tại A gọi I là trung điểm của BC . Gọi M,N lần lượt là hình chiếu của I nên AB,AC
a) Chúng minh AMIN là hình vuông
Cho ▲ABC vuông cân tại A gọi I là trung điểm của BC . Gọi M,N lần lượt là hình chiếu của I nên AB,AC
a) Chúng minh AMIN là hình vuông
b) Chứng minh MN//BC
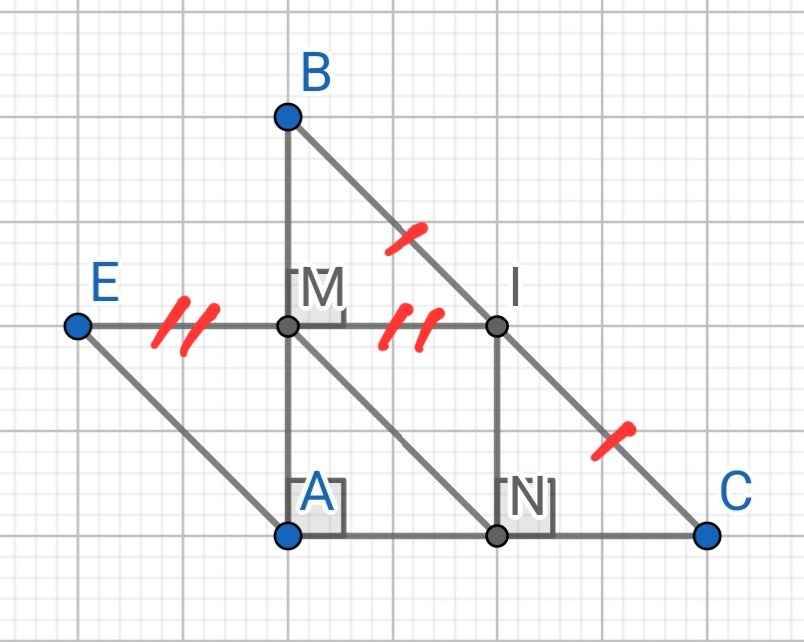
c) Gọi E đối xứng vs I qua M ? t/g AEMN là hình gì
a) Do IM ⊥ AB (gt)
⇒ IM //AC
Mà I là trung điểm BC
⇒ M là trung điểm AB
⇒ IM là đường trung bình của ∆ABC
⇒ IM = AC/2
Do IN ⊥ AC (gt)
IN // AB
Mà I là trung điểm BC
⇒ N là trung điểm AC
⇒ AN = AC/2
⇒ IM = AC/2 = AN
Do IM // AC
⇒ IM // AN
Do M là trung điểm AB (cmt)
⇒ AM = IM = AB/2
Xét tứ giác AMIN có:
IM // AN (cmt)
IM = AN (cmt)
⇒ AMIN là hình bình hành
Mà ∠MAN = 90⁰ (∆ABC vuông tại A)
⇒ AMIN là hình chữ nhật
Lại có AM = IM (cmt)
⇒ AMIN là hình vuông
b) Do M là trung điểm AB (cmt)
N là trung điểm AC (cmt)
⇒ MN là đường trung bình của ∆ABC
⇒ MN // BC
c) Do E đối xứng với I qua M (gt)
⇒ ME = IM
⇒ ME = AN
Do IM // AN (cmt)
⇒ ME // AN
Xét tứ giác AEMN có:
ME // AN (cmt)
ME = AN (cmt)
⇒ AEMN là hình bình hành
chị ơi em chx học đường trung bình
Cho ▲ABC vuông cân tại A gọi I là trung điểm của BC . Gọi M,N lần lượt là hình chiếu của I nên AB,AC
b) Chứng minh MN//BC
Dựa và ý a)
Có \(\dfrac{IM}{AC}=\dfrac{BI}{BC}=\dfrac{1}{2}\) ( định lý thales )
mà IM // AC ( cùng vuông góc với AB )
\(\Rightarrow\) IM là đường trung bình của tam giác ABC mà I là trung điểm của BC
\(\Rightarrow\) M là trung điểm của AB
Lại có \(\dfrac{IN}{AB}=\dfrac{IC}{CB}=\dfrac{1}{2}\) ( đly thales )
mà IN // AB ( cùng vuông góc với AC )
\(\Rightarrow\) IN là đường tb của tam giác ABC
mà I là trung điểm của BC nên N là trung điểm của AC
Có M và N lần lượt là trung điểm của AB và AC
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
Suy ra MN // BC
hình bạn tự vẽ nhé:
ta có: AI=BI(tính chất đừng trung tuyến trong tg vuông)
=>tg AIB cân tại I
=>góc IAB= góc IBA (1)
ta lại có :
góc IAB=góc NMA(tính chất 2 đ chéo trong hcn) (2)
từ (1) (2) suy ra góc NMA=góc IBA
mà 2 góc này ở vị trí đồng vị
suy ra MN//BC
Cho tam giác ABC vuông cân tại A, AH là đường cao . Gọi M là điểm bất kì trên cạnh BC . Gọi I , K lần lượt là hình chiếu của M trên cạnh AB , AC . Chứng minh tam giác IHK vuông cân
Cho tam giác ABC vuông cân tại A. Gọi I,K lần lượt là trung điểm của AB và AC. Gọi H,D lần lượt là hình chiếu của I và A lên BK, M là hình chiếu của A trên HI, O là giao điểm của BM và AC
a, C/m tam giác DAK = tam giác HBI
b, C/m tam giác BMH vuông cân
c, Tính góc ADC
d, Gọi P là giao điểm của MD và AB. C/m OP vuông góc với BC
Cho tam giác ABC vuông tại A có AB<AC. N là trung điểm BC. Gọi M, P lần lượt là hình chiếu của N trên AB, AC. Lấy E sao cho P là trung điểm của NE.
a) Chứng minh M,P lần lượt là trung điểm của AB, AC
b) Tứ giác ANCE là hình gì ( chứng minh hình)
a: Xét ΔCAB có
N là trung điểm của AB
NP//AB
=>P là trung điểm của AC
Xét ΔCAB có
N là trung điểm của BC
NM//AC
=>M là trung điểm của AB
b: Xét tứ giác ANCE có
P là trung điểm chung của AC và NE
AC vuông góc NE
=>ANCE là hình thoi
cho tam giác ABC vuông tại A có đường cao AH, gọi EF lần lượt là hình chiếu của H lên AB và AC a) chứng minh AH=EF b) gọi M là trung điểm của BC chứng minh AM vuông góc với EF c) gọi I,J lần lượt là trung điểm của HB, HC chứng ming tứ giác IEFJ là hình thang vuông
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=FE
Cho tam giác ABC vuông tại A (AB<AC).Gọi I là tđiểm của BC . Qua I kẻ các đg thẳng song song với AC và AB chúng lần lượt cắt AB tại M ,cắt AC tại N ...a)Chứng MINH các từ giác AMIN,,MNIB là hình j vì sao? b)Vẽ AH vuông góc với BC tại H . Tính góc MHN giúp mình ik cảm ơn
Cho tam giác ABC vuông cân tại A, có AH là đường cao. Gọi M là một điểm bất kì trên cạnh BC, I và K lần lượt là hình chiếu vuông góc của M trên AB, AC. Chứng minh tam giác IHK vuông cân.
Không mất tính tổng quát, ta xét M thuộc HC (trường hợp M thuộc HB tương tự)
Tam giác ABC vuông tại A có đường cao AH xuất phát từ đỉnh A nên \(AH=\frac{1}{2}BC\) (1) và AH cũng là đường trung tuyến \(\Rightarrow HC=HB=\frac{1}{2}BC\) (2) và đường phân giác => ^CAH = ^BAH. Từ (1) và (2) suy ra \(\Delta\)AHC vuông cân tại H. Từ đó
AH = HC và ^ACH = ^HAC = ^BAH. Tới đây tìm cách chứng minh AI = CK(mình chưa biết làm đâu:v). Từ đó suy ra \(\Delta\)HIA = \(\Delta\)HKC. Suy ra ^AHI = ^CHK suy ra ^IHK = ^IHA + ^AHK = ^CHK + ^AHK = 90o => \(\Delta\)IHK vuông tại H (3)
Mặt khác từ \(\Delta\)HIA = \(\Delta\)HKC suy ra HI =HK suy ra \(\Delta\)IHK cân tại H (4)
Từ (3) và (4) suy ra đpcm.
P/s: Ko chắc, bác zZz Cool Kid zZz check giúp:v
làm đoạn tth thiếu nhé:
cm AI=CK
t/g ABC vuông cân tại A => ABC^=45 độ
t/g BIM có I^=90 độ mà ABC^=45 độ => BMI^=45 độ
=> t/g BIM vuông cân tại I => BI=IM
Mà tứ giác BIAK có I^=A^=K^=90 độ => tứ giác BIAK là HCN => IM=AK=BI
Mà AB=AC
=> AB-BI=AC-AK
=> AI=CK
Chứng minh AI=CK
Ta có:
Tứ giác KMIA có 3 góc vuông nên nó là hình chữ nhật.Khi đó thì AI=KM.(1)
Tam giác KMC có ^K=900,^C=450 nên nó là tam giác vuông cân.
=>KC=KM (2)
Từ (1);(2) suy ra đpcm.
Hân hạnh mời god tth check hộ ạ.Ko chắc lắm đâu nha BÁC.
Cho tam giác ABC vuông tại A, AK là đường cao. Gọi M,N lần lượt là hình chiếu của K trên AB, AC. Gọi D là trung điểm AB và I là điểm đối xứng của A qua K. Chứng minh CD vuông góc IN