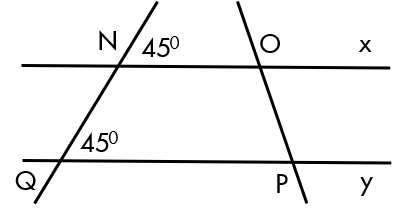
a) (0,5 điểm) Sử dụng thước thẳng, ê ke hoặc thước đo góc vẽ lại hình trên vào bài làm.
b) (1,0 điểm) Chứng minh rằng $\widehat{{NOP}}+\widehat{{QPO}}=180^{\circ}$.
Hình học (2 điểm)
Vẽ đoạn thẳng $AB$ dài $4$ cm, lấy điểm $M$ là trung điểm của đoạn thẳng $AB$.
a) Tính đoạn thẳng $AM$ và $MB$.
b) Vẽ tia $Mx$ sao cho $\widehat{AMx}= 50^{\circ}$, vẽ tia $My$ sao cho $\widehat{BMy}= 70^{\circ}$. Sử dụng thước đo góc để đo số đo $\widehat{xMy}$.
Bạn tự vẽ hình.
a, M là trung điểm AB
=> \(AM=MB=\frac{AB}{2}=\frac{4}{2}=2\left(cm\right)\)
b, Mình không có thước đo góc nên mình tính luôn nhé.
\(\widehat{AMx}+\widehat{xMy}+\widehat{BMy}=180^o\) (góc bẹt)
=> \(\widehat{xMy}=60^o\)
a, vì điểm M là trung điểm của đoạn thẳng AB
suy ra$ AM=MB=/dfrac{AB}2=\dfrac 42=2(cm)
b, -> trường hợp 1: xMy=60•
-> trường hợp 2: xMy=160•
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.

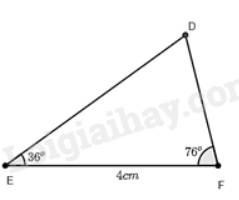
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
Cho \(\widehat {xOy} = 120^\circ \). Vẽ tia phân giác của góc xOy bằng 2 cách:
a) Sử dụng thước thẳng và compa; b) Sử dụng thước hai lề
Vẽ góc \(\widehat {xOy} = 120^\circ \)
a) Sử dụng thước thẳng và compa
Bước 1: Trên tia Ox, lấy điểm A bất kì ( A khác O); vẽ một phần đường tròn tâm O, bán kính OA, cắt tia Oy tại điểm B.
Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.
Bước 3: Vẽ một phần đường tròn tâm B bán kính BO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.
Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.
b) Sử dụng thước hai lề
Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Ox, dùng bút vạch một vạch thẳng theo cạnh của thước.
Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Oy, dùng bút vạch một vạch thẳng theo cạnh của thước.
Bước 3: Hai nét vạch thẳng vẽ ở bước 1 và bước 2 cắt nhau tại điểm C nằm trong góc xOy.
Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.
Vẽ tia phân giác Oz của xOy có số đo bằng 68\(^\circ \), sử dụng thước đo góc theo hướng dẫn. Nếu Oz là toa phân giác của góc xOy thì \(\widehat {xOz} = \frac{1}{2}.68^\circ = 34^\circ \). Ta có cách vẽ sau:
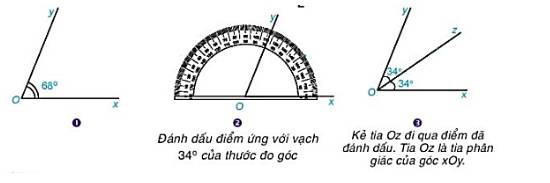
Bước 1. Vẽ góc xOy có số đo bằng \(68^0\)
Bước 2. Sử dụng thước đo độ, đánh dấu điểm ứng với vạch \(34^0\) của thước đo góc.
Bước 3. Kẻ tia Oz đi qua điểm đã đánh dấu. Tia Oz là tia phân giác của góc xOy.

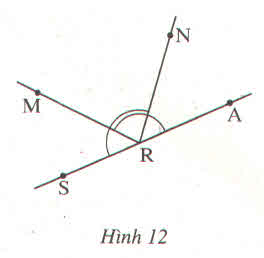
a) Vẽ hình 12 trong đó 3 điểm S, R, A thẳng hàng và \(\widehat{ARM}=\widehat{SRN}=130^0\)
b) Tính \(\widehat{ARN},\widehat{MRS},\widehat{MRN}\)
c) Dùng thước đo góc kiểm tra lại kết quả
b: \(\widehat{MRS}=180^0-130^0=50^0\)
\(\widehat{ARN}=180^0-130^0=50^0\)
\(\widehat{MRN}=180^0-50^0-50^0=80^0\)
Thước đo góc ở Hình 5.4 có điểm gì khác với thước đo góc thường sử dụng vẽ trên giấy?

Độ bền sản phẩm cao, vật liệu cao cấp. Vạch chia và thang đo rõ nét, có vít vặn lớn để cố định vị trí cho kết quả đo nhanh và chính xác.
Thước đo ở hình 5.4 khác với thước đo góc thường sử dụng trên giấy là đây là thước đo góc vạn năng.
Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN với các kích thước như Hình 66. Bạn Hoa đố bạn Thanh vẽ điểm P thỏa mãn \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) mà không sử dụng thước đo góc. Em hãy giúp bạn Thanh sử dụng thước thẳng (có chia khoảng milimét) và compa để vẽ điểm P và giải thích kết quả tìm được.
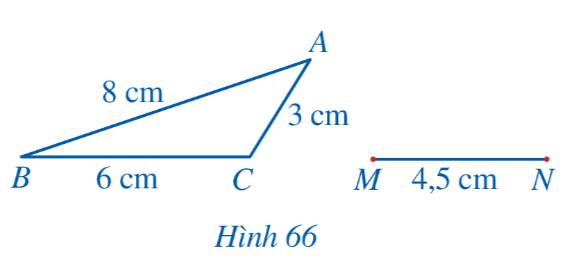
Vì tổng ba góc trong một tam giác bằng \(180^\circ \) nên nếu \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) thì \(\widehat {MPN} = \widehat {CBA}\)
Ta cần \(\Delta ABC \backsim\Delta NPM\)
Khi đó \(\frac{{AB}}{{NP}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{NM}}\) hay \(\frac{8}{{NP}} = \frac{6}{{PM}} = \frac{3}{{4,5}} = \frac{2}{3}\)
Ta có: \(\frac{8}{{NP}} = \frac{2}{3} \Rightarrow NP = 8.3:2 = 12cm\)
\(\frac{6}{{MP}} = \frac{2}{3} \Rightarrow MP = 6.3:2 = 9cm\)
Vậy Thanh cần dùng thước kẻ vẽ hai đoạn thẳng NP=12cm và PM=9cm để tìm được điểm P thỏa mãn yêu cầu đề bài.
Những loại thước đo mà em biết
A .Ê ke, ke vuông, thước đo góc vạn năng
B.Thước đo góc vạn năng ,ke vuông
C.Ke vuông ,thước đo góc vạn năng ,thước cặp
D.Thước cặp thước đo góc vạn năng Ê ke,ke vuông