b: \(\widehat{MRS}=180^0-130^0=50^0\)
\(\widehat{ARN}=180^0-130^0=50^0\)
\(\widehat{MRN}=180^0-50^0-50^0=80^0\)
b: \(\widehat{MRS}=180^0-130^0=50^0\)
\(\widehat{ARN}=180^0-130^0=50^0\)
\(\widehat{MRN}=180^0-50^0-50^0=80^0\)
Vẽ góc cho biết một cạnh và số đo góc đó trong bốn trường hợp sau :
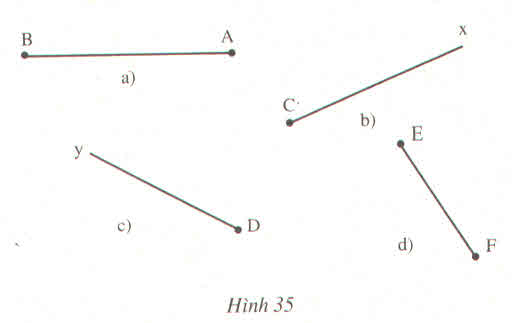
a) \(\widehat{BAC}=20^0\)
b) \(\widehat{xXz}=110^0\)
c) \(\widehat{yDx}=80^0\)
d) \(\widehat{EFy}=145^0\)
Vẽ từng hình theo mỗi cách diễn đạt sau :
a) Hai góc xOy và yOz kề bù, với \(\widehat{xOy}=135^0\)
b) Hai góc mOn và nOt kề nhau và phụ nhau, với \(\widehat{nOm}=30^0\)
c) Cho tia Ap. Vẽ \(\widehat{qAp}=30^0\)
d) Cho tia Bt. Vẽ \(\widehat{rBt}=90^0\)
e) Cho tia Ck. Vẽ \(\widehat{hCk}=45^0\)
Vẽ liên tiếp các hình theo cách diễn đạt sau :
a) \(\widehat{nAx}=180^0\)
b) \(\widehat{mAx}=135^0\)
c) \(\widehat{kAx}=45^0\), tia Ak nằm trong góc xAm
d) \(\widehat{nAy}=90^0\), tia Ay nằm trong góc xAm
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết \(\widehat{xOt}=30^0,\widehat{yOt'}=60^0\). Tính số đo các góc \(\widehat{yOt},\widehat{tOt'}\) ?
Trên cùng một nửa mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho \(\widehat{BOA}=45^0,\widehat{COA}=55^0\). Tính số đo góc BOC ?
a) Vẽ góc \(40^0\) có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình
b) Đóng hai chiếc đinh vào điểm A và B cách nhau 2,5cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1;M_2;M_3;....\) khác nhau của đỉnh M. Vậy ta có :
\(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=.....=40^0\)
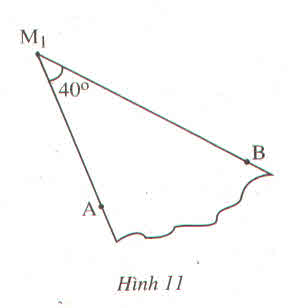
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (h.11)
Vẽ \(\widehat{mOn}=30^0\). Vẽ tiếp góc nOp kề bù với góc mOn. Vẽ tiếp góc pOq phụ với góc mOn đồng thời tia Oq nằm trong góc nOp. Cho biết số đo của góc nOq ?
Vẽ góc xBy có số đo bằng \(45^0\)
Hướng dẫn : Vẽ tia Bx, sau đó trên một nửa mặt phẳng có bờ chứa tia Bx vẽ tia By sao cho \(\widehat{xBy}=45^0\)
Cho Ot nằm giữa 2 tia Ox và Oy, biết \(\widehat{xOy}\)= 600, \(\widehat{xOt}\) = 1100. So sánh góc xOt và góc tOy