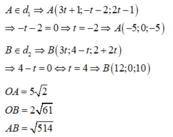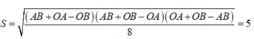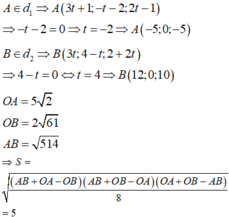Trong mặt phẳng oxy cho hai đường thẳng d1:2x-y+1=0, d2:x-y-2=0. gọi A,B là hai điểm có tọa độ nguyên lần lượt nằm trên d1 và d2 sao cho tam giác OAB vuông cân tại O. Tính diện tích tam giác OAB

Những câu hỏi liên quan
cho ba đường thẳng d1:y=3x,d2:y=1/3x,d3:y=-x+4 a,vẽ d1,d2,d3 trên cùng mặt phẳng toạ độ b,gọia,b lần lượt là giao điểm của d1 và d2.tìm toạ độ của a và b c,chứng minh tam giác OAB cân d,tính diện tích tam giác OAB
a: 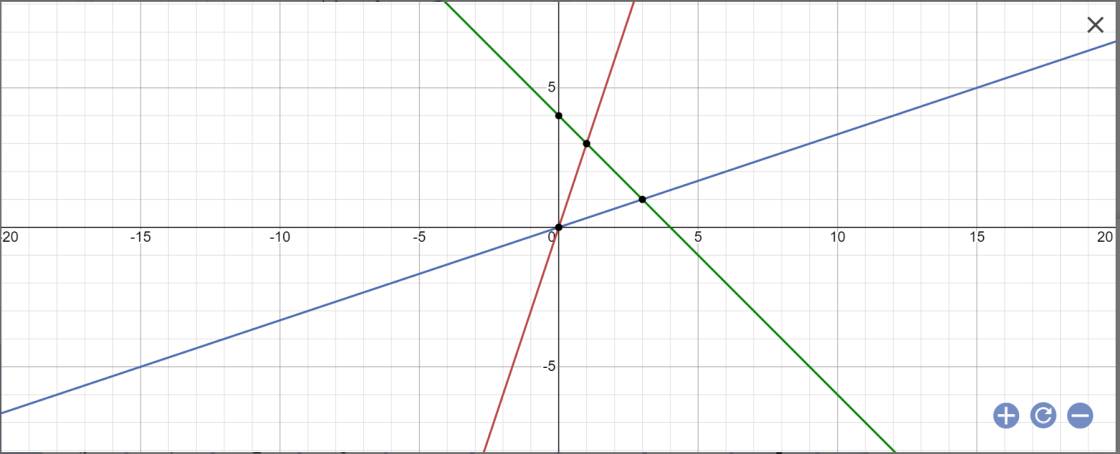
b:
Bổ sung đề: A,B lần lượt là giao của (d1) với (d2) và (d3)
Tọa độ A là:
3x=1/3x và y=3x
=>x=0 và y=0
Tọa độ B là:
3x=-x+4 và y=3x
=>x=1 và y=3
Đúng 0
Bình luận (0)
Cho 3 đường thẳng d1: y3x; d2: ydfrac{1}{3}; d3: y-x+4a) Vẽ d1, d2 ,d3 trên cùng mặt phẳng tọa độ. b) Gọi A, B lần lượt là giao điểm của d3 với d1, d2.Tìm tọa độ của A và B.c) Chứng minh tam giác OAB cân.d) Tính các góc trong tam giác OAB (làm tròn đến độ).Mọi người giúp em với ạ.Em cảm ơn!
Đọc tiếp
Cho 3 đường thẳng d1: y=3x; d2: y=\(\dfrac{1}{3}\); d3: y=-x+4
a) Vẽ d1, d2 ,d3 trên cùng mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của d3 với d1, d2.Tìm tọa độ của A và B.
c) Chứng minh tam giác OAB cân.
d) Tính các góc trong tam giác OAB (làm tròn đến độ).
Mọi người giúp em với ạ.
Em cảm ơn!
b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
1
3
y
+
2
-
1
z
+
1
2
;
d
2
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d 1 : x - 1 3 = y + 2 - 1 = z + 1 2 ; d 2 : x = 3 t y = 4 - t z = 2 + 2 t
và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B.
Diện tích S của tam giác OAB bằng
A. S = 5
B. S = 3
C. S = 6
D. S = 10
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
−
1
3
y
+
2
−
1
z
+
1
2
;
d
2
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 ; d 2 : x = 3 t y = 4 − t z = 2 + 2 t và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B. Diện tích S của tam giác OAB bằng bao nhiêu?
A. S = 5
B. S = 3
C. S = 6
D. S = 10
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
−
1
3
y
+
2
−
1
z
+
1
2
;
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 ; d 2 : x = 3 t y = 4 − t z = 2 + 2 t và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B. Diện tích S của tam giác OAB bằng bao nhiêu?
A. S = 5.
B. S = 3.
C. S = 6.
D. S = 10.
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Đúng 1
Bình luận (0)
trong mặt phẳng tọa độ oxy cho hai đường thẳng (d1)2x-y+5=0 và (d2) x+y-3=0 cắt nhau tại i. phương trình đường thẳng đi qua m (-2;0) cắt d1, d2 tại a, b sao cho tam giác iab cân tại a có phương trình dạng ax+by+2=0. tính t=a-5b
Trong mặt phẳng tọa độ Oxy cho điểm M(1,-1)và hai đường thẳng có phương trình (d1):x - y - 1 = 0 và (d2) 2x+y-5=0. Gọi A là giao điểm của 2 đường thẳng trên . Biết rằng có 2 đường thẳng (d) đi qua M cắt 2 đường thẳng trên tại B,C sao cho tam giác ABC có BC=3AB .Tìm phương trình đường thẳng của 2 đường thẳng đó
cho 3 đường thẳng d:y=3x,d1:y=-1/3x và d2;y=-x+4
a) vẽ 3 đường thẳng trên cùng 1 mptd
b)gọi giao điểm của d với d1 và d2 lần lượt là A và B.Tìm tọa độ giao điểm của A và B
c)CM:tam giác OAB vuông
d)Tính các góc của tam giác OAB
Trên mặt phẳng tọa độ Oxy cho hai đường thẳng :
(d1) : y = -2x +4 và (d2) : y = \(\dfrac{1}{2}\)x + b ( b>0)
Gọi A là giao điểm của (d1) với (d2) ; B,C lần lượt là giao điểm của Ox với (d1), (d2) . Tìm giá trị của b để AO là tia phân giác của góc BAC