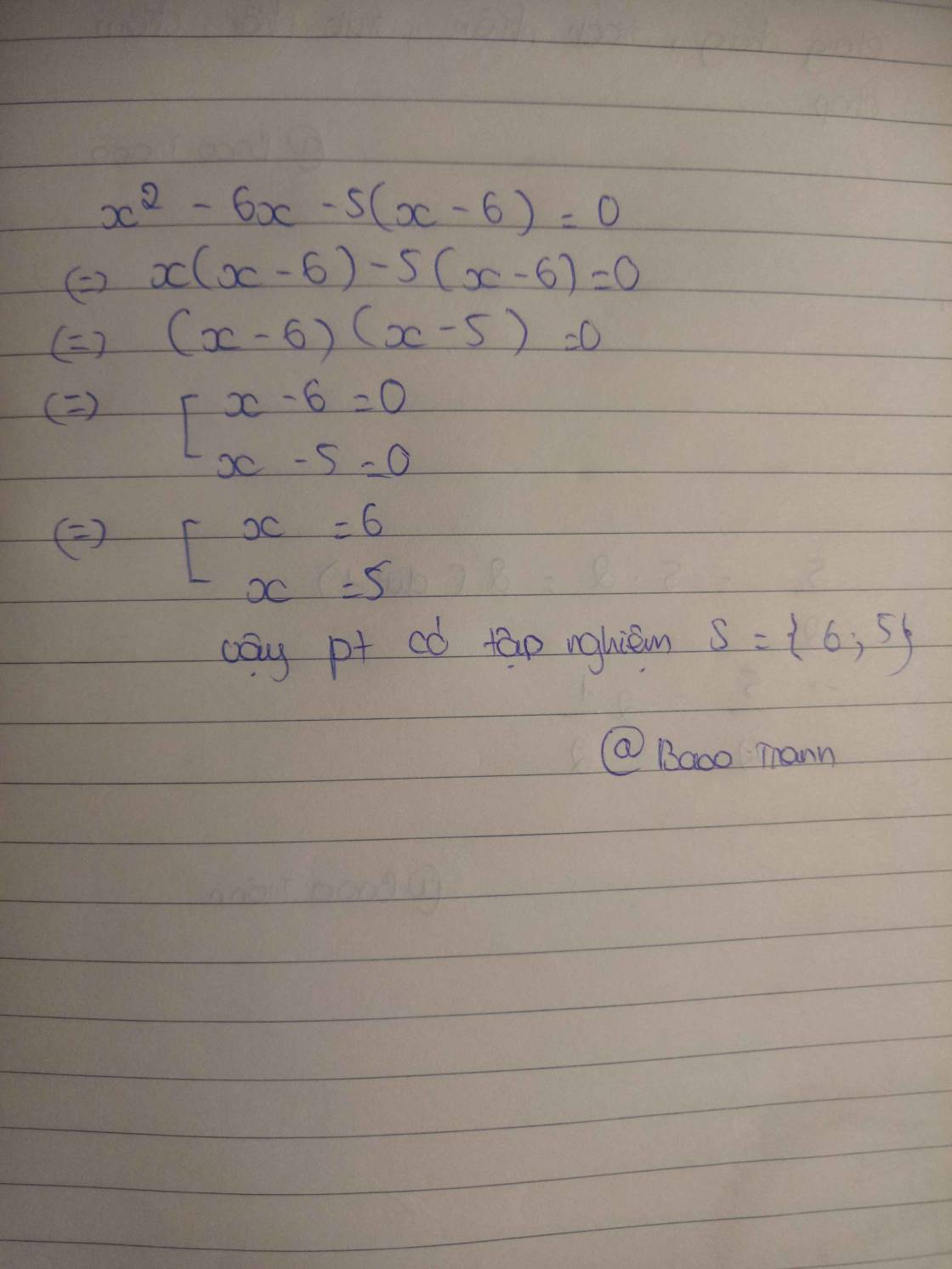vì \(5+x^2\ge5\left(\forall x\in R\right)\) 

=>6x-3=0

=>x=\(\dfrac{1}{2}\)

KL:S=\(\dfrac{1}{2}\)

=>x(x-6)-5(x-6)=0

=>(x-6)(x-5)=0

=>x=5 hoặc x=6

a.

\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow-1\le x\le3\)

b.

ĐKXĐ: \(x\ge0\)

\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)

\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)

\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)

\(\Leftrightarrow2x^2-8x+5=0\)

\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)

Câu b còn 1 cách giải nữa:

Với \(x=0\) không phải nghiệm

Với \(x>0\) , chia 2 vế cho \(\sqrt{x}\) ta được:

\(\sqrt{2x+8+\dfrac{5}{x}}+\sqrt{2x-4+\dfrac{5}{x}}=6\)

Đặt \(\sqrt{2x-4+\dfrac{5}{x}}=t>0\Leftrightarrow2x+8+\dfrac{5}{x}=t^2+12\)

Phương trình trở thành:

\(\sqrt{t^2+12}+t=6\)

\(\Leftrightarrow\sqrt{t^2+12}=6-t\)

\(\Leftrightarrow\left\{{}\begin{matrix}6-t\ge0\\t^2+12=\left(6-t\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}t\le6\\12t=24\end{matrix}\right.\)

\(\Rightarrow t=2\)

\(\Rightarrow\sqrt{2x-4+\dfrac{5}{x}}=2\)

\(\Leftrightarrow2x-4+\dfrac{5}{x}=4\)

\(\Rightarrow2x^2-8x+5=0\)

\(\Leftrightarrow...\)

a, Do  \(x=-4\)là một nghiệm của pt trên nên 

Thay \(x=-4\)vào pt trên pt có dạng : 

\(16+4m-10m+2=0\Leftrightarrow-6m=-18\Leftrightarrow m=3\)

Thay m = 3 vào pt, pt có dạng : \(x^2-3x-28=0\)

\(\Delta=9-4.\left(-28\right)=9+112=121>0\)

vậy pt có 2 nghiệm pb : \(x_1=\frac{3-11}{2}=-\frac{8}{2}=-4;x_2=\frac{3+11}{2}=7\)

b, Theo Vi et : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=6\\x_1x_2=\frac{c}{a}=7\end{cases}}\)

Vậy m=3, và ngiệm còn lại x₂=7

a)

m = 3

x₂=7

ĐKXĐ: $x \geq 2$

\(\Leftrightarrow2\left(x-4\right).\sqrt{x-2}-2\left(x-4\right)+\left(x-2\right)\sqrt{x+1}-2\left(x-2\right)+6x-18=0\\ \Leftrightarrow2.\left(x-4\right).\dfrac{x-3}{\sqrt{x-2}+1}+\left(x-2\right).\dfrac{x-3}{\sqrt{x+1}+2}+6.\left(x-3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(\dfrac{2.\left(x-4\right)}{\sqrt{x-2}+1}+\dfrac{x-2}{\sqrt{x+1}+2}+6=0\right)\\ \Leftrightarrow x=3\)

Vì \(\dfrac{2.\left(x-4\right)}{\sqrt{x-2}+1}+\dfrac{x-2}{\sqrt{x+1}+2}+6=\dfrac{2\left(x-4\right)+4.\sqrt{x-2}+4}{\sqrt{x-2}+1}+\dfrac{x-2}{\sqrt{x+1}+2}+2\\ =\dfrac{2\left(x-2\right)+4.\sqrt{x-2}}{\sqrt{x-2}+1}+\dfrac{x-2}{\sqrt{x+1}+2}+2>0\)

Vậy....

1, Thay m=6 vào pt ta có:

\(x^2-\left(6-2\right)x-6+5=0\\ \Leftrightarrow x^2-4x-1=0\)

\(\Delta=\left(-4\right)^2-4.1.\left(-1\right)=16+4=20\)

\(x_1=\dfrac{4+2\sqrt{5}}{2}=2+\sqrt{5},x_2=\dfrac{4-2\sqrt{5}}{2}=2-\sqrt{5}\)

\(2,\Delta=\left[-\left(m-2\right)\right]^2-4\left(-m+5\right)\\ =m^2-4m+4+4m-20\\ =m^2-16\)

Để pt có 2 nghiệm phân biệt thì

\(\Delta>0\\ \Leftrightarrow m^2-16>0\\ \Leftrightarrow\left[{}\begin{matrix}m>4\\m< -4\end{matrix}\right.\)

a) Tam thức \(f(x) =  - 5{x^2} + x - 1\) có \(\Delta  =  - 19 < 0\), hệ số \(a =  - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm

b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta  = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)

Suy ra bất phương trình có nghiệm duy nhất là x = 4

c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta  =  - 23 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm.