a, Với m= 2, ta có 2 x 2 − 4 x + 2 = 0 ⇔ x = 1                                              

b) Phương trình (1) có hai nghiệm  x 1 , x 2  khi và chỉ khi  Δ ' ≥ 0 ⇔ − 2 ≤ m ≤ 2

Theo Vi-et , ta có:  x 1 + x 2 = m          1 x 1 . x 2 = m 2 − 2 2    2

Theo đề bài ta có:  A = 2 x 1 x 2 − x 1 − x 2 − 4 = m 2 − 2 − m − 4 = m − 3 m + 2

Do  − 2 ≤ m ≤ 2  nên  m + 2 ≥ 0 ,  m − 3 ≤ 0 . Suy ra  A = m + 2 − m + 3 = − m 2 + m + 6 = − m − 1 2 2 + 25 4 ≤ 25 4

Vậy  MaxA = 25 4  khi  m = 1 2 .

a: Khi m=2 thì pt (1) trở thành:

\(x^2-4x+3=0\)

=>(x-1)(x-3)=0

=>x=1 hoặc x=3

\(a\)) Thay \(:m=2\)

\(Pt\rightarrow x^2-4x+3=0\\ \rightarrow\left(x-1\right)\left(x-3\right)=0\\ \rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

b) Để phương trình có nghiệm

\(\rightarrow m^2-m^2+m-1\ge0\\ \rightarrow\ge1\)

\(Vi-et:\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-m+1\end{matrix}\right.\)

\(x_1\)\(^2\)\(+2mx9=9\)

\(\rightarrow x_1\)\(^2+\left(x_1+x_2\right)x_2=9\)

\(\rightarrow x_1\)\(^2+x_1x_2+x_2\)\(^2=9\)

\(\rightarrow x_1\)\(^2+2x_1x_2+x_2\)\(^2-x_1x_2=9\)

\(\rightarrow\left(x_1+x_2\right)^2-x_1x_2=9\)

\(\rightarrow4m^2-m^2+m-1=9\\ \rightarrow3m^2+m-1=9\\ \rightarrow\left[{}\begin{matrix}m=\dfrac{5}{3}\\m=-2\left(l\right)\end{matrix}\right.\)

a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)

pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\) 

Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)

b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)

Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).

Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)

Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)

Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)

1) Với m= 2 PT trở thành  x 2 − 4 x + 3 = 0  

Giải phương trình tìm được các nghiệm  x = 1 ;   x = 3.  

2) Ta có  Δ ' = m 2 − m 2 + 1 = 1 > 0 , ∀ m .  

Do đó, phương trình (1) luôn có hai nghiệm phân biệt.

Từ giả thiết ta có x i 2 − 2 m x i + m 2 − 1 = 0 , i = 1 ; 2. x i 3 − 2 m x i 2 + m 2 x i − 2 = x i x i 2 − 2 m x i + m 2 − 1 + x i − 2 = x i − 2 , i = 1 ; 2.  

Áp dụng định lí Viét cho phương trình (1) ta có  x 1 + x 2 = 2 m ; x 1 . x 2 = m 2 − 1  

Ta có

  x 1 − 2 + x 2 − 2 = 2 m − 4 ; x 1 − 2 x 2 − 2 = x 1 x 2 − 2 x 1 + x 2 + 4 = m 2 − 1 − 4 m + 4 = m 2 − 4 m + 3

Vậy phương trình bậc hai nhận  x 1 3 − 2 m x 1 2 + m 2 x 1 − 2 ,   x 2 3 − 2 m x 2 2 + m 2 x 2 − 2  là nghiệm là x 2 − 2 m − 4 x + m 2 − 4 m + 3 = 0.

a, Thay m=3 vào pt ta có:

\(\left(1\right)\Leftrightarrow x^2-6x+4=0\\ \Leftrightarrow x=3\pm\sqrt{5}\)

b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)

\(\Leftrightarrow\left(-m\right)^2-1.4\ge0\\ \Leftrightarrow m^2-4\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4\end{matrix}\right.\)

\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=2\\ \Leftrightarrow x^2_1+2x_1+1+x^2_2+2x_2+1=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=0\\ \Leftrightarrow\left(2m\right)^2-2.4+2.2m=0\\ \Leftrightarrow4m^2+4m-8=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)

bài này sử dụng định lí vi-ét nha

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)

\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)

\(b,\left(m-1\right)x^2-2mx+m-2=0\)

\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)

\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)

\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)

\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)

\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Chọn D

Đặt  t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:

t²+ 2(1-m) t+ m²- 3 m+2= 0  (2)

Để pt (1) có nghiệm x ≥ 1 khi và chi khi pt (2) có nghiệm t ≥ 0

+ TH1: Pt (2) có nghiệm t₁ ≤ 0 ≤ t₂

Khi đó; P= t₁.t₂ ≤ 0 hay m²- 3m+ 2 ≤ 0

Từ đó; 1≤ m≤ 2

+ TH2: Pt (2) có nghiệm :

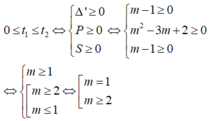
Kết luận: với  thì pt (1) có nghiệm x ≥ 1

a) Với m=1,ta có:

x²-2.1.x+2.1-2=0

<=> x²-2x=0

<=> x(x-2)=0

<=> x=0 hoặc x-2=0

<=> x=0 hoặc x=2