Cho tam giác nhọn ABC, 2 đường cao BD và CE cắt tại H
CM: AD.CB=ED.AB
Những câu hỏi liên quan
Cho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H. Chứng minh tam giác ABD đồng dạng tam giác ACECho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H.a) CM: Tam giác ABD đồng dạng tam giác ACE.b) CM: HB.HDHC.HEc) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMCgóc ANB90 độ. CMR: AMAN.
Đọc tiếp
Cho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H. Chứng minh tam giác ABD đồng dạng tam giác ACECho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H.
a) CM: Tam giác ABD đồng dạng tam giác ACE.
b) CM: HB.HD=HC.HE
c) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC=góc ANB=90 độ. CMR: AM=AN.
a) CM: Tam giác ABD đồng dạng tam giác ACE.
b) CM: HB.HD=HC.HE
c) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC=góc ANB=90 độ. CMR: AM=AN.
Cho tam giác nhọn ABC Các đường cao BD và CE cắt nhau tại H biết HB = 6 cm HC = 9 cm và BD+ CE = 20 cm Tính độ dài BD và CE
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn tâm (O) . Đường cao BD và đường cao CE cắt nhau tại H , BD cắt CE tại F, AF cắt đường tròn (O) tại K.
a, Cm : tứ giác BCDE nội tiếp, xác định tâm đường tròn.
b, cm : FA .FK = FE.FD;
c. CM : FH vuông góc với AM
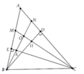
Mình sửa lại đề: Cho tam giác ABC nhọn (AB < AC) nội tiếp (O). Đường cao BD, CE cắt nhau tại H. EF cắt BC tại F. AF cắt lại (O) tại K. Gọi M là trung điểm của BC.
a) Từ gt dễ thấy tứ giác BCDE nội tiếp đường tròn tâm M.
b) Tứ giác BCDE nội tiếp nên theo phương tích ta có FB . FC = FD . FE.
Tứ giác AKBC nội tiếp nên theo phương tích ta có FK . FA = FB . FC.
Vậy ta có đpcm.
c) Ta có FA . FK = FE . FD nên theo phương tích đảo ta có tứ giác AKED nội tiếp.
Gọi giao điểm thứ hai của đường tròn đường kính AH và FH là N.
Khi đó FH . FN = FE . FD = FB . FC.
Suy ra tứ giác BHNC nội tiếp.
Ta có \(\widehat{DNC}=360^o-\widehat{DNH}-\widehat{CNH}=\left(180^o-\widehat{DNH}\right)+\left(180^o-\widehat{CNH}\right)=\widehat{DEH}+\widehat{HBC}=2\widehat{HBC}=\widehat{DMC}\).
Do đó tứ giác DNMC nội tiếp.
Tương tự tứ giác ENMB nội tiếp.
Suy ra \(\widehat{DNM}+\widehat{DNA}=180^o-\widehat{ACB}+\widehat{AED}=180^o\) nên A, N, M thẳng hàng.
Từ đó \(\widehat{MHN}=\widehat{ANH}=90^o\) nên \(FH\perp AM\).
(Câu c là trường hợp đặc biệt của định lý Brocard khi tứ giác BEDC nội tiếp đường tròn tâm M).
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A , góc A nhọn. Đường cao BD và CE cắt nhau tại H, vẽ điểm M là trung điểm của BC. Cm: a)BD CE. b)ED // BC. c)Giao điểm A, H, M thẳng hàng. ...
Đọc tiếp
Cho tam giác ABC cân tại A , góc A nhọn. Đường cao BD và CE cắt nhau tại H, vẽ điểm M là trung điểm của BC. Cm: a)BD = CE. b)ED // BC. c)Giao điểm A, H, M thẳng hàng. d)ED < BC.
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có:
AB = AC (ΔABC cân tại A)
∠BAD chung
⇒ ΔABD = ΔACE (cạnh huyền - góc nhọn)
⇒ BD = CE (hai cạnh tương ứng)
Vậy BD = CE
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC các đường cao BD, CE. Tia phân giác của góc ABD cắt AC và AB theo thứ tự tại N và M, tia BN cắt CE tại K. Tia CM cắt BD tại H. Chứng minh BN vuông góc với CM
Cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O. Các đường cao BD và CE của tam giác cắt nhau tại H (D thuộc AC. E thuộc AB) 1. CM các tứ giác ADHE và BCDE nội tiếp được trong một đường tròn 2. Tia BD và tia CE lần lượt cắt đường tròn O tại M và N. Cm DE song song MN 3. Kẻ đường kính AK. Cm tứ giác BKCM là hình thang cân
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc
A
B
D
^
v
à
A
C
E
^
cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:a) BN ^ CM;b) Tứ giác MNFIK là hình thoi
Đọc tiếp
Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc A B D ^ v à A C E ^ cắt nhau tại O, và lần lượt cắt AC, AB tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H: Chứng minh rằng:
a) BN ^ CM;
b) Tứ giác MNFIK là hình thoi
a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a có 2 đường cao BD và CE cắt nhâu tại H a, CM: BDCE b, CM: tam giác BHC cân c, CM: AH là đường trung trực của BC d, Trên tia BD lấy điểm K sao cho D là trung điểm BK So sánh góc ECB và góc DKC
Đọc tiếp
cho tam giác abc cân tại a có 2 đường cao BD và CE cắt nhâu tại H a, CM: BD=CE b, CM: tam giác BHC cân c, CM: AH là đường trung trực của BC d, Trên tia BD lấy điểm K sao cho D là trung điểm BK So sánh góc ECB và góc DKC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà BD=CE
nên BEDC là hình thang cân
b: góc ABD+góc DBC=góc ABC
góc ACE+góc ECB=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc DBC=góc ECB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Chứng minh: P, H. BD + CH. CE = BC2.