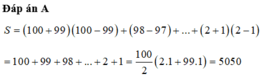992 - 982 +972 - 962 +...+ 32 - 22 +1

Những câu hỏi liên quan
Tính: A=99^2-98^2+97^2-96^2+...+3^2-2^2+1A=992−982+972−962+...+32−22+1 ta được kết quả là
A=(99-98)(99+98)+...+(3-2)(3+2)+1
=99+98+...+3+2+1
=100*99/2=4950
Đúng 0
Bình luận (0)
M = 1002– 992 + 982 – 972 + … + 22 – 12;
N = (202+ 182 + 162 + … + 42 + 22) – (192 + 172 + 152 + … + 32 + 12);
P = (-1)n.(-1)2n+1.(-1)n+1.
a:
Số số hạng trong dãy M là:
(1002-12):10+1=100(số)
=>Sẽ có 50 cặp (1002;992); (982;972);....;(22;12) có hiệu bằng 10
\(M=1002-992+982-972+...+22-12\)
\(=\left(1002-992\right)+\left(982-972\right)+...+\left(22-12\right)\)
\(=10+10+...+10\)
=10*50=500
b: \(N=\left(202+182+...+42+22\right)-\left(192+172+...+32+12\right)\)
\(=\left(202-192\right)+\left(182-172\right)+...+\left(22-12\right)\)
=10+10+...+10
=10*10=100
Đúng 0
Bình luận (0)
Tính tổng
S
100
2
−
99
2
+
98
2
−
97
2
+
....
+
2
2
−
1
2
A. 5050 B. 4949 C. 10100 D. 9898
Đọc tiếp
Tính tổng S = 100 2 − 99 2 + 98 2 − 97 2 + .... + 2 2 − 1 2
A. 5050
B. 4949
C. 10100
D. 9898
Tính tổng S = 1002 – 992 +982 – 972 + … + 22 – 12
A.1290
B 5160
C. 5587
D. 5050
Chọn D.
S = 1002 – 992 +982 – 972 + … + 22 – 12
= (100 – 99)(100 + 99) + (98 – 97)(98 + 97) + … + (2-1)(2+1)
= 199 + 195 + … + 3
Ta có dãy số 3, 7, …, 195, 199 là cấp số cộng với công sai d = 4, số hạng đầu tiên u1 = 3 và số hạng n là un = 199.
Do đó có 199 = 3 + (n – 1).4 ⇒ n = 50.
Vậy 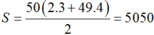 .
.
Đúng 0
Bình luận (0)
Thực hiện phép tính:
1002 - 992 + 982 - 972 +...+ 22 - 12
\(100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
\(=199+195+...+3\)
Số lượng số hạng:
\(\left(199-3\right):4+1=50\) (số hạng)
Tổng:
\(\left(3+199\right)\times50:2=5050\)
Đúng 2
Bình luận (0)
Lời giải:
$=(100^2-99^2)+(98^2-97^2)+....+(2^2-1^2)$
$=(100-99)(100+99)+(98-97)(98+97)+...+(2-1)(2+1)$
$=100+99+98+97+...+2+1=100(100+1):2=5050$
Đúng 1
Bình luận (0)
Rút gọn các biểu thức sau: A = 1002 - 992 + 982 - 972 + ... + 22 - 12.
a. A = 1002 - 992+ 982 - 972 + ... + 22 - 12
b. B = 3(22 + 1) (24 + 1) ... (264 + 1) + 12
c. C = (a + b + c)2 + (a + b - c)2 - 2(a + b)2
Rút gọn ạ
a: A=(100-99)(100+99)+(98-97)(98+97)+...+(2-1)(2+1)
=100+99+98+...+2+1
=5050
b: \(B=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)+1\)
\(=\left(2^4-1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)+1\)
\(=\left(2^8-1\right)\left(2^8+1\right)\cdot...\cdot\left(2^{64}+1\right)\)+1
\(=2^{64}-1+1=2^{64}\)
Đúng 3
Bình luận (0)
1. Rút gọn các biểu thức sau:
A = 1002- 992 + 982 - 972 + ... + 22 - 12
B = 3(22+ 1) (24 + 1) ... (264 + 1) + 1
C = (a + b + c)2+ (a + b - c)2 - 2(a + b)2
Rút gọn các biểu thức sau:
a. A = 1002 - 992+ 982 - 972 + ... + 22 - 12
b. B = 3(22 + 1) (24 + 1) ... (264 + 1) + 12
c. C = (a + b + c)2 + (a + b - c)2 - 2(a + b)2
\(A=\left(100-99\right)\left(100+99\right)+\left(99-98\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\\ A=100+99+99+98+...+2+1\\ A=\left(100+1\right)\left(100-1+1\right):2=5050\)
\(B=\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{64}+1\right)+1\\ B=\left(2^1-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)...\left(2^{64}+1\right)+1\\ B=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)...\left(2^{64}+1\right)+1\\ B=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)...\left(2^{64}+1\right)+1\\ B=\left(2^{16}-1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)+1\\ B=\left(2^{32}-1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)+1\\ B=\left(2^{64}-1\right)\left(2^{64}+1\right)+1=2^{128}-1+1=2^{128}\)
\(C=a^2+b^2+c^2+2ab+2bc+2ac+a^2+b^2+c^2+2ab-2ac-2bc-2a^2-4ab-2b^2\\ C=2c^2\)
Đúng 6
Bình luận (0)
1. Rút gọn các biểu thức sau:
a. A = 1002 - 992+ 982 - 972 + ... + 22 - 12
b. B = 3(22 + 1) (24 + 1) ... (264 + 1) + 12
c. C = (a + b + c)2 + (a + b - c)2 - 2(a + b)2
a: \(A=\left(100-99\right)\left(100+99\right)+\left(98+97\right)\left(98-97\right)+....+\left(2+1\right)\left(2-1\right)\)
\(=100+99+98+97+...+2+1\)
=5050
b: \(B=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)+1\)
\(=\left(2^4-1\right)\left(2^4+1\right)\cdot...\cdot\left(2^{64}+1\right)+1\)
\(=\left(2^8-1\right)\left(2^8+1\right)\cdot...\cdot\left(2^{64}+1\right)+1\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)+1\)
\(=\left(2^{32}-1\right)\left(2^{32}+1\right)\left(2^{64}+1\right)+1\)
\(=\left(2^{64}-1\right)\cdot\left(2^{64}+1\right)+1\)
\(=2^{128}-1+1=2^{128}\)
Đúng 2
Bình luận (0)
a. \(A=100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
\(=199+195+...+3\)
\(=\dfrac{\left(199+3\right)\left(\dfrac{199-3}{4}+1\right)}{2}=5050\)
b. \(B=3\left(2^2+1\right)\left(2^4+1\right)...\left(2^{64}+1\right)+1^2\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{64}+1\right)+1^2\)
\(=\left(2^4-1\right)\left(2^4+1\right)...\left(2^{64}+1\right)+1^2\)
\(=2^{128}-1+1=2^{128}\)
c) \(C=\left(a+b+c\right)^2+\left(a+b-c\right)^2-2\left(a+b\right)^2\)
\(=a^2+b^2+c^2+2ab+2ac+2bc+a^2+b^2+c^2+2ab-2ac-2bc-2a^2-2b^2-4ab\)
\(=2c^2\)
Đúng 0
Bình luận (0)