Trong mặt phẳng 0xy , cho 3 đường thẳng d1 : x+2y+1=0 ; d2 : x+y-5=0 và d3 : 2x+3y-10=0 . Phương trình đường thẳng delta đi qua giao điểm của d1d2 và song song với d3 là

Những câu hỏi liên quan
Trong mặt phẳng 0xy , cho đường thẳng d : x-2y+1=0 và điểm M(2;-2) . Toạ độ hình chiếu vuông góc của điểm M lên đường thẳng d là
Phương trình d' qua M và vuông góc d có dạng:
\(2\left(x-2\right)+1\left(y+2\right)=0\Leftrightarrow2x+y-2=0\)
Hình chiếu vuông góc của M lên d là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\) \(\Rightarrow\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
Đúng 0
Bình luận (0)
câu 1a) A4sqrt{24}-3sqrt{54}+5sqrt{6}-sqrt{150}b) Bsqrt{14+4sqrt{10}}-dfrac{1}{sqrt{10}+3}câu 2 trong mặt phẳng tọa độ 0xy cho đường thẳng (d1): y2x và đường thẳng (d2): y-x+2a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độb) cho đường thẳng (d3): yax+b. xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2), đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1
Đọc tiếp
câu 1
a) \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
b) \(B=\sqrt{14+4\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
câu 2 trong mặt phẳng tọa độ 0xy cho đường thẳng (d1): y=2x và đường thẳng (d2): y=-x+2
a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ
b) cho đường thẳng (d3): y=ax+b. xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2), đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1
Câu 1:
a: \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
\(=4\cdot2\sqrt{6}-3\cdot3\sqrt{6}+5\sqrt{6}-5\sqrt{6}\)
\(=8\sqrt{6}-9\sqrt{6}=-\sqrt{6}\)
b: \(B=\sqrt{14+4\cdot\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
\(=\sqrt{10+2\cdot\sqrt{10}\cdot2+4}-\dfrac{\left(\sqrt{10}-3\right)}{10-9}\)
\(=\sqrt{\left(\sqrt{10}+2\right)^2}-\sqrt{10}+3\)
\(=\sqrt{10}+2-\sqrt{10}+3=5\)
Câu 2:
a:
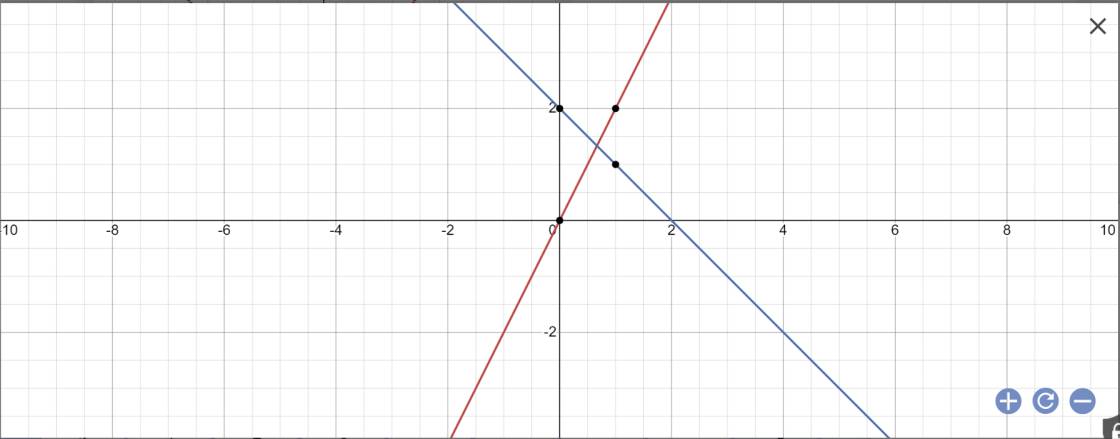
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
vậy: (d3): y=-x+3
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho điểm D(6;2) và hai đường thẳng (d1): x-2y+1=0; (d2): x+2y-3=0. Viết phương trình đường thẳng \(\left(\Delta\right)\) đi qua D và cắt hai đường thẳng (d1); (d2) tại hai điểm B; C sao cho tam giác tạo bởi ba đường thẳng (d1); (d2); \(\left(\Delta\right)\) là tam giác cân, với BC là cạnh đáy.
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 ; d 2 : x - 5 - 1 = y + 1 2 = z - 2 1 và mặt phẳng (P): x + 2y + 3z - 5 = 0. Đường thẳng vuông góc với (P), cắt d 1 , d 2 có phương trình là
A. x - 1 1 = y + 1 2 = z 3
B. x - 2 1 = y - 3 2 = z - 1 3
C. x - 3 1 = y - 3 2 = z + 2 3
D. x - 1 3 = y + 1 2 = z 1
Viết lại phương trình
d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1
d 2 : x - 5 - 1 = y + 1 2 = z - 2 1
Giả sử đường thẳng cần tìm là ∆ cắt hai đường thẳng
d 1 , d 2 lần lượt tại A ( 3 - t; 3 - 2t; -2 + t ) và B ( 5 - 3t'; -1 + 2t; 2 + t' )
Một véctơ chỉ phương của ∆ là
u ∆ → = A B → = 2 - 3 t ' + t ; - 4 + 2 t ' + 2 t ; 4 + t ' - t
Một véctơ pháp tuyến của (P) là
n P → = 1 ; 2 ; 3 t a co u ∆ → = k n nên ta có hệ
2 - 3 t ' + t = k - 4 + 2 t ' + 2 t = 2 k 4 + t ' - t = 3 k ⇔ - 3 t ' + t - k = - 2 2 t ' + 2 t - 2 k = 4 t ' - t - 3 k = - 4 ⇔ t ' = 1 t = 2 k = 1
Suy ra A ( 1;-1;0 ) và B ( 2;1;3 ) u ∆ → 2 ; 1 ; 3 do đó
∆ : x - 1 1 = y + 1 2 = z 3
Đáp án cần chọn là A
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho 2 đường thẳng
d
1
:
x
+
3
2
y
+
2
-
1
z
+
2
-
4...
Đọc tiếp
Trong không gian Oxyz cho 2 đường thẳng d 1 : x + 3 2 = y + 2 - 1 = z + 2 - 4 ; d 2 : x + 1 3 = y + 1 2 = z - 2 3 và mặt phẳng ( P ) : x + 2 y + 3 z - 7 = 0 Đường thẳng vuông góc với mặt phẳng (P), cắt d 1 và d 2 có phương trình là:

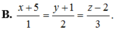
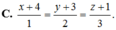
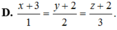
Đáp án B.
Gọi ![]()
thuộc
d
1
và ![]()
thuộc d 2 là 2 giao điểm.
Ta có: ![]()
Vì M N → cùng phương với
![]() nên ta có:
nên ta có:
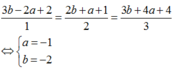
![]() điểm này thuộc đường thẳng ở đáp án B.
điểm này thuộc đường thẳng ở đáp án B.
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho hai đường thẳng
d
1
:
x
−
3
−
1
y
−
3
−
2
z
+
2
1
,
d
2...
Đọc tiếp
Trong không gian Oxyz cho hai đường thẳng d 1 : x − 3 − 1 = y − 3 − 2 = z + 2 1 , d 2 : x − 5 − 3 = y + 1 2 = z − 2 1 và mặt phẳng P : x + 2 y + 3 z − 5 = 0 . Đường thẳng vuông góc với (P) cắt d 1 và d 2 có phương trình là
A. x − 1 1 = y + 1 2 = z 3 .
B. x − 2 1 = y − 3 2 = z − 1 3 .
C. x − 3 1 = y − 3 2 = z + 2 3 .
D. x − 1 3 = y + 1 2 = z 1 .
Đáp án A.
Giả sử đường thẳng d cắt d 1 , d 2 lần lượt
M , N ⇒ M 3 − t 1 ; 3 + 2 t 1 ; − 2 + t 1 , N 5 − 3 t 2 ; − 1 + 2 t 2 ; 2 + t 2
Ta có
M N → = t 1 − 3 t 2 + 2 ; 2 t 1 + 2 t 2 − 4 ; − t 1 + t 2 + 4
và n p → = 1 ; 2 ; 3
Mà d vuông góc với P nên
M N → = k n p → ⇒ t 1 − 3 t 2 + 2 = k 2 t 1 + 2 t 2 − 4 = 2 k − t 1 + t 2 + 4 = 3 k ⇔ t 1 = 2 t 2 = 1 k = 1 ⇒ M 1 ; − 1 ; 0 N 2 ; 1 ; 3
Ta có M N → = 1 ; 2 ; 3 ⇒ d : x − 1 1 = y + 1 2 = z 3 .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng (P):x+2y+3z-70 và hai đường thẳng
d
1
:
x
+
3
2
y
+
2
-
1
z
+
2
-
4
;...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P):x+2y+3z-7=0 và hai đường thẳng d 1 : x + 3 2 = y + 2 - 1 = z + 2 - 4 ; d 2 : x + 1 3 = y + 1 2 = z - 2 3 Đường thẳng vuông góc với mặt phẳng (P) và cắt cả hai đường thẳng d1 và d2 có phương trình là
A. x + 7 1 = y 2 = z - 6 3
B. x + 5 1 = y + 1 2 = z - 2 3
C. x + 4 1 = y + 3 2 = z + 1 3
D. x + 3 1 = y + 2 2 = z + 2 3
Trong không gian Oxyz cho 2 đường thẳng
d
1
:
x
+
3
2
y
+
2
−
1
z
+
2
−
4
,
d
2...
Đọc tiếp
Trong không gian Oxyz cho 2 đường thẳng
d 1 : x + 3 2 = y + 2 − 1 = z + 2 − 4 , d 2 : x + 1 3 = y + 1 2 = z − 2 3 và mặt phẳng P : x + 2 y + 3 z − 7 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d 1 và d 2 có phương trình là
A. x + 7 1 = y 2 = z − 6 3 .
B. x + 5 1 = y + 1 2 = z − 2 3 .
C. x + 4 1 = y + 3 2 = z + 1 3 .
D. x + 3 1 = y + 2 2 = z + 2 3 .
Đáp án B.
Gọi M 2 a − 3 ; − 2 − a ; − 2 − 4 a thuộc d 1 và N − 1 + 3 b ; − 1 + 2 b ; 2 + 3 b thuộc d 2 là 2 giao điểm.
Ta có:
M N → = 3 b − 2 a + 2 ; 2 b + a + 1 ; 3 b + 4 a + a .
Vì M N → cùng phương với n P → = 1 ; 2 ; 3 nên ta có:
3 b − 2 a + 2 1 = 2 b + a + 1 2 = 3 b + 4 a + 4 3 ⇔ a = − 1 b = − 2
⇒ M − 5 ; − 1 ; 2 , điểm này thuộc đường thẳng ở đáp án B.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
,...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 , d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P): x +2y +3z -5 =0. Đường thẳng vuông góc với (P), cắt cả d 1 v à d 2 có phương trình là
A. x - 1 3 = y + 1 2 = z 1
B. x - 2 1 = y - 3 2 = z - 1 3
C. x - 1 1 = y + 1 2 = z 3
D. x - 3 1 = y - 3 2 = z + 2 3
Xét vị trí của d và d1, d và d2.
Đáp án C
Đúng 0
Bình luận (0)









