Cho △ABC, góc A = 90 độ. M∈AC, vẽ đg tròn đường kính MC. BM căt đường tròn tại Q. QA cắt đường tròn tại F
CMR:a) Tg ABCQ,ABEM nội tiếp
b)góc ABQ= góc ACQ
c)CA là phân giác góc FCB
Những câu hỏi liên quan
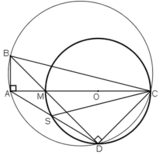
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp
b) góc ABD bằng góc ACD
c) CA là tia phân giác của góc SCB
a)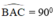 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
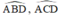đều là góc nội tiếp chắn cung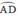 
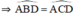
c) + Trong đường tròn đường kính MC:
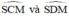đều là các góc nội tiếp cùng chắn cung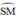 
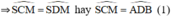
+ Trong đường tròn đường kính BC:
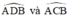đều là các góc nội tiếp chắn cung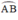 
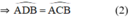
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AC AB). Trên đoạn AC lấy điểm M và vẽ đường tròn đường kính MC. Tia BM cắt đường tròn tại D. Đường thẳng AD cắt đường tròn tại S.a. C/m: ABCD là tứ giác nội tiếp.b. C/m: CA là phân giác của góc SCB.c. Gọi H là giao điểm thứ hai của đường tròn đường kính MC với BC. C/m: các đường thẳng AB; MH; CD đồng qui.d. Biết CM a; Cˆ 300. Tính diện tích hình quạt OMmH ( với cung MmH là cung nhỏ.)e. C/m : M là tâm đường tròn nội tiếp tam giác ADH.f. ...
Đọc tiếp
Cho tam giác ABC vuông tại A (AC > AB). Trên đoạn AC lấy điểm M và vẽ đường tròn đường kính MC. Tia BM cắt đường tròn tại D. Đường thẳng AD cắt đường tròn tại S.
a. C/m: ABCD là tứ giác nội tiếp.
b. C/m: CA là phân giác của góc SCB.
c. Gọi H là giao điểm thứ hai của đường tròn đường kính MC với BC. C/m: các đường thẳng AB; MH; CD đồng qui.
d. Biết CM = a; Cˆ = 300. Tính diện tích hình quạt OMmH ( với cung MmH là cung nhỏ.)
e. C/m : M là tâm đường tròn nội tiếp tam giác ADH.
f. ABˆC = 720 ; BCˆD = 73o tính các góc của tam giác AHD
g. Trong trường hợp DA là tiếp tuyến của đường tròn đường kính MC thì M ở vị trí nào?
a: góc MDC=1/2*sđ cung MC=90 độ
=>góc BDC=90 độ
Xét tứ giác ABCD có
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
b: ABCD nội tiếp
=>góc BCA=góc BDA
=>góc BCA=góc SCA
=>CA là phân giác của góc SCB
c: Gọi N là giao của MH với AB
góc MHC=1/2*180=90 độ
=>NH vuông góc BC
Xét ΔCBN có
NH,CA là đường cao
NH cắt CA tại M
=>M là trực tâm
=>BM vuông góc CN
=>C,D,N thẳng hàng
=>MH,CD,BA đồng quy
Đúng 0
Bình luận (0)
Cho tam giác ABC ( góc A = 90 độ ) trẹn AC lấy điểm M sao cho AM < MC. Vẽ Đường tròn O' đường kính CM. Đường thẳng BM cắt O tại D, AD kéo dài cắt O tại S.
a) Chứng mình BADC nội tiếp
b ) BC cắt O tại E. CM: ME phân giác góc AED
c) CM: CA p.giác góc BCS
d) Cho đướng tròn bán kính R, AM = 1/2 AC và góc BCA = 30 độ. Tính d.tích tứ giác MECS theo R
Cho △ ABC vuông tại A, với AC > AB. Trên AC lấy một điểm M, vẽ đường tròn (O) đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S
a. Chứng minh ABCD là tứ giác nội tiếp.
B. Chứng minh góc ABD = góc ABD
C. Chứng minh CA là tia phân giác của góc. AOB bằng 75°
cho tam giác ABC vuông ở A, trên cạnh AC lấy điểm M vẽ đường tròn đường kính MC. Nối BM kéo dài cắt đường tròn tại D doạn thẳng AD cắt đường tròn ở K . CMR :
a) ABCD là tứ giác nội tiếp
b) CA là tia phân giác góc KCB
Xét (O) có
ΔCDM nội tiếp
CM là đường kính
DO đó: ΔCDM vuông tại D
Xét tứ giác ABCD có
\(\widehat{CDB}=\widehat{CAB}=90^0\)
Do đó: ABCD là tứ giác nội tiếp
b: \(\widehat{BCA}=\widehat{ADB}\)
mà \(\widehat{ADB}=\widehat{KCA}\)
nên \(\widehat{BCA}=\widehat{KCA}\)
hay CA là tia phân giác của góc KCB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông ở A, trên cạnh AC lấy điểm M vẽ đường tròn đường kính MC. Nối BM kéo dài cắt đường tròn tại D doạn thẳng AD cắt đường tròn ở K . CMR :
a) ABCD là tứ giác nội tiếp
b) CA là tia phân giác góc KCB
Xét (O) có
ΔCDM nội tiếp
CM là đường kính
DO đó: ΔCDM vuông tại D
Xét tứ giác ABCD có
ˆCDB=ˆCAB=900CDB^=CAB^=900
Do đó: ABCD là tứ giác nội tiếp
b: ˆBCA=ˆADBBCA^=ADB^
mà ˆADB=ˆKCAADB^=KCA^
nên ˆBCA=ˆKCABCA^=KCA^
hay CA là tia phân giác của góc KCB
Đúng 0
Bình luận (0)
Cho tam giác ABC (góc A=90 độ).Lấy điểm M trên cạnh AC(M khác A khác C).Đường tròn đường kính MC cắt đường thẳng BM và BC lần lượt tại D và N,đường thẳng AD cắt đường tròn tại điểm thứ hai là S
a)Tứ giác ABCD nội tiếp,xác định tâm và bán kính
b)CA là phân giác của góc SCB
c)Ba đường thẳng AB,MN,CD đồng quy
giúp mình với ạ;-;
a: Xét (O) có
ΔMDC nội tiếp
MC là đường kính
=>ΔMDC vuông tại D
góc CAB=góc CDB=90 đọ
=>ABCD nội tiếp
b: góc SCA=góc ADB
góc ADB=góc ACB
=>góc SCA=góc ACB
=>CA là phân giác của góc SCB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp;
b) \(\widehat{ABD}=\widehat{ACD};\)
c) CA là tia phân giác của góc SCB.
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB
Đúng 1
Bình luận (0)
a) Ta có:\(\widehat{BAC}=90^o\) ⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
đều là góc nội tiếp chắn cung 
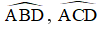
c) + Trong đường tròn đường kính MC:
đều là các góc nội tiếp cùng chắn cung 
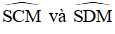
+ Trong đường tròn đường kính BD:
đều là các góc nội tiếp chắn cung 
Đúng 1
Bình luận (0)
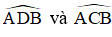
Cho điểm M thuộc cạnh a của tam giác ABC vuông tại A Vẽ đường tròn O đường kính MC cắt BC tại E D BM cắt đường tròn O tại D tia AD cắt đường tròn O tại E AE cắt đường tròn O tại f Chứng minh câu a tứ giác ABCD nội tiếp K là phân giác góc s a b c a b c d đồng quy câu d d m là phân giác góc ade câu a m là tâm đường tròn nội tiếp tam giác hde f d f song song AB