Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của AB, BC và AC. Chứng minh DH =EF.

Những câu hỏi liên quan
Cho tam giác ABC có đường cao AH (H thuộc BC). Gọi E, F lần lượt là trung điểm của AB, AC
a) Chứng minh AH ^ EF.
b) EF cắt AH tại K. Chứng minh KA = KH.
a: Ta có: ΔAHB vuông tại H
mà HE là đường trung tuyến ứng với cạnh huyền AB
nên HE=AE
hay E nằm trên đường trung trực của AH(1)
Ta có: ΔAHC vuông tại H
mà HF là đường trung tuyến ứng với cạnh huyền AC
nên HF=FA
hay F nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra FE là đường trung trực của AH
hay FE\(\perp\)AH
Đúng 2
Bình luận (0)
Bài 4: Cho tam giác ABC. Gọi D là trung điểm của AB, E là trung điểm của BC. Biết AC = 8cm. DE Tính
Bài 5: Cho tam giác ABC vuông tại A (AB<AC), đường cao AH Tử H vẽ HE và HF lần lượt vuông góc với AB và AC (E = AB Fe AD.
a) Chứng minh AH = EF b) Trên tia FC xác định điểm K sao cho FK = AF. Chứng minh tử giác EHKF là hinh binh hành
Cho tam giác ABC vuông tại A, AH là đường cao ( H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC).
a) Chứng minh AH = EF.
b) Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC tại I.Chứng minh tứ giác AOIK là hình bình hành.
c) EF cắt IK tại M. Chứng minh tam giác OMI cân
Cho tam giác ABC vuông tại A, AH là đường cao ( H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC).
a) Chứng minh AH = EF.
b) Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC tại I.Chứng minh tứ giác AOIK là hình bình hành.
c) EF cắt IK tại M. Chứng minh tam giác OMI cân
a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>AH=EF
b: góc IFE=90 độ
=>góc IFH+góc EFH=90 độ
=>góc IFH+góc AHF=90 độ
=>góc IFH=góc IHF
=>IH=IF và góc IFC=góc ICF
=>IH=IC
=>I là trung điểm của HC
Xét ΔHAC có HO/HA=HI/HC
nên OI//AC và OI=AC/2
=>OI//AK và OI=AK
=>AOIK là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AH là đường cao (H thuộc BC). Kẻ HE, HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC). a)Chứng minh AH=EF.
b)Gọi O là giao điểm của AH và EF, K là trung điểm của AC. Qua F kẻ đường thẳng vuông góc với EF cắt BC ở I. Chứng minh tứ giác AOIK là hình bình hành
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
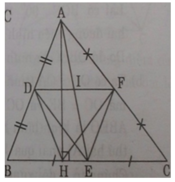
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)
Cho tam giác ABC có AH là đường cao. Gọi E và F lần lượt là trung điểm của AB và AC. đoạn thẳng AHI. điểm của a)Biết BC = 6 cm, Tỉnh độ dài EF. b)Đoạn thẳng EF cắt AH tại I. Chứng minh: I là trung điểm AH
Bài 23 : Cho tam giác ABC vuông tại A ( AB AC ) . Gọi F là trung điểm của BC , qua F kẻ đường thẳng d vuông góc và BC , đường thẳng d cắt đường thẳng AB , AC lần lượt tại D và E. a ) Chứng minh : tam giác AED đồng dạng với tam giác PEC b ) Chứng minh , BF.FC DF.EF c ) Tính BC biết DE 5cm , EF 4cm . d ) Gọi K là giao điểm của BE và DC , đường thẳng FK cắt AC tại I. Chứng minh : AC. EI AE . IC .Bài 26 : Cho tam giác ABC vuông tại A , đường cao AH . Gọi E , F lần lượt là chân đường vuông g...
Đọc tiếp
Bài 23 : Cho tam giác ABC vuông tại A ( AB < AC ) . Gọi F là trung điểm của BC , qua F kẻ đường thẳng d vuông góc và BC , đường thẳng d cắt đường thẳng AB , AC lần lượt tại D và E.
a ) Chứng minh : tam giác AED đồng dạng với tam giác PEC
b ) Chứng minh , BF.FC = DF.EF
c ) Tính BC biết DE = 5cm , EF = 4cm
. d ) Gọi K là giao điểm của BE và DC , đường thẳng FK cắt AC tại I. Chứng minh : AC. EI = AE . IC
.Bài 26 : Cho tam giác ABC vuông tại A , đường cao AH . Gọi E , F lần lượt là chân đường vuông góc kẻ tử H đến AB , AC
a ) Chứng minh : AH = EF
b ) Chứng minh : AB^2 = BH.BC
c ) Chứng minh :tam giác HEF đồng dạng vớ itam giác ABC
d ) Kẻ tìa Bx vuông góc BC , Bx cắt đường thẳng AC tại K. Gọi O là giao điểm của EF và AH . Chứng minh : CO đi qua trung điểm của KB .
Bài 27 : Cho tam giác ABC có góc A = 90 độ ; AB = 15cm , AC = 20cm , đường phân giác BD cắt đường cao AH tại K.
a ) Tính BC , AD
b ) Chứng minh tam giác AHB đồng dạng với tam giác CAB ,
c ) Chứng minh : BH.BD = BK.BA , d ) Gọi M là trung điểm của KD . Kẻ tia Bx song song với AM . Tia Bx cắt tia AH tại J , Chứng minh : HK.AJ = AK.HJ .
Bài 26 : Bài giải
a. Do
là hình chữ nhật
Bài 27 : Bài giải
Hình :
Còn bài giải tham khảo : Câu hỏi của nguyễn nhật trang nhung - Toán lớp 8 - Học toán với OnlineMath
Câu hỏi của nguyễn nhật trang nhung - Toán lớp 8 - Học toán với OnlineMath
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
BC2 = AB2 + AC2
⇔ BC2 = 152 + 202 = 625
⇔ B C = √ 625 = 25 cm
Δ ABC có BD là phân giác góc ABC ⇒ \(\dfrac{AD}{AB}\) = \(\dfrac{DC}{BC}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{AD}{AB}=\dfrac{DC
}{BC}=\dfrac{AD+DC}{AB+BC}=\dfrac{20}{40}=\dfrac{1}{2}\)
suy ra: \(\dfrac{AD}{AB}=\dfrac{1}{2}\)⇒AD=7,5cm
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC ( AB<AC), đường cao AH. Gọi D,E,F lần lượt là trung điểm của BC, CA,AB.
a. Chứng minh EF là đường trung trực của AH
B Tứ giác DEFH là hình gì? Vì sao?
Giúp mình với!
Mình đag cần gấp!!


















