a + a = a x a = b
b x a = x : a = b
x : b = a + 0 = a
Hỏi a ; b và x là những số nào
Cho mệnh đề chứa biến: 2-3x > x-192−3x>x−19. Tìm hai giá trị nguyên a,a, bb thuộc khoảng (-10;10)(−10;10) sao cho x = ax=a thì mệnh đề đúng, x= bx=b thì mệnh đề sai.
bn nào viết rõ hơn giùm mik đc ko.
(a^2+b^2)(x^2+y^2)=(ax+by)^2
<=> a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 = a^2x^2 + 2abxy + b^2y^2
<=> a^2y^2 + b^2x^2 = 2abxy
<=> a^2y^2 + b^2x^2 - 2abxy = 0
<=> (ay - bx)^2 = 0
=> ay - bx = 0
=> ay = bx
=> a/x = b/y ( x,y khác 0)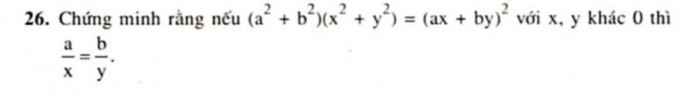
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
a/ab x 9=a1b
b/a x bxba=aaa
c/a,b x 9,9=aa,bb
Chứng minh rằng nếu phương trình a x 2 + bx + c = x (a ≠ 0) vô nghiệm thì phương trình a a x 2 + b x + c 2 + b(a x 2 + bx + c) + c = x cũng vô nghiệm.
Cho A={x∈N/x²<4}; B={x∈N/(5x-3x²)(x²-2x-3)=0}
a) hãy liệt kê các tập hợp của A và B
b) tìm A∩B;A∪B;A\B
GIẢI GẤP GIÚP E Ạ
a)
A={0; 1}
B={0; 3}
b) A∩B={0}. A∪B={0; 1; 3}. A\B={1}
Cho mệnh đề chứa biến: 3-2x > 3x-83−2x>3x−8. Tìm hai giá trị nguyên a,a, bb thuộc khoảng (-10;10)(−10;10) sao cho x = ax=a thì mệnh đề đúng, x= bx=b thì mệnh đề sai.
Cho đa thức A(x)=ax2+bx+c
a) Chứng tỏ A(2).A(-1)<0 , biết 5a+b+2c=0
b) Cho A(x)=0 với mọi x . Chứng minh a=b=c=0
a)Mình nghĩ là chứng minh \(A\left(2\right).A\left(-1\right)\le0\)mới đúng chớ! Mình làm theo đề đã sửa nhé!
Ta có: \(A\left(2\right)=4a+2b+c\)
\(A\left(-1\right)=a-b+c\)
Suy ra \(A\left(2\right)+A\left(-1\right)=5a+b+2c=0\)
Suy ra \(A\left(2\right)=-A\left(-1\right)\)
Thay vào,ta có: \(A\left(2\right).A\left(-1\right)=-\left[A\left(-1\right)\right]^2\le0\) (đúng)
b)Theo đề bài A(x) = 0 với mọi x nên:
\(A\left(1\right)=a+b+c=0\Rightarrow a=-b-c\) (1)
\(A\left(-1\right)=a-b+c=0\Rightarrow b=a+c\) (2)
Cộng (1) và (2) lại,ta được: \(a+b=a-b\Leftrightarrow2b=0\Leftrightarrow b=0\) (*)
Khi đó \(A\left(x\right)=ax^2+c=0\forall x\)
\(\Rightarrow A\left(1\right)=a+c=0\Rightarrow a=-c\) (3)
\(A\left(2\right)=4a+c=0\Leftrightarrow-4a=c\) (4)
Cộng theo vế (3) và (4) suy ra \(-3a=0\Leftrightarrow a=0\) (**)
Thay a = b = 0 vào,ta có: \(A\left(x\right)=c=0\forall x\)(***)
Từ (*);(**) và (***) ta có a = b =c = 0 (đpcm)
Đúng ko ta?
a, Chứng tỏ rằng nếu a + b + c = 0 thì x = 1 là một nghiệm của đa thức P(x) = ax2 + bx + c
b, Chứng tỏ rằng nếu a – b + c = 0 thì x = -1 là một nghiệm của đa thức Q(x) = ax2 + bx + c
$\rm x=1\\\to ax^2+bx+c=a+b+c=0\\\to x=1\,\là \,\,no \,\pt$
Cho đa thức \(P(x) = a{x^2} + bx + c\)(a ≠ 0). Chứng tỏ rằng:
a) \(P(0) = c\); b) \(P(1) = a + b + c\); c) \(P( - 1) = a - b + c\)
a) Thay x = 0 vào đa thức P(x) ta được:
\(P(0) = a{.0^2} + b.0 + c = 0 + 0 + c = c\). Vậy \(P(0) = c\).
b) Thay x = 1 vào đa thức P(x) ta được:
\(P(0) = a{.1^2} + b.1 + c = a + b + c\). Vậy \(P(1) = a + b + c\).
c) Thay x = – 1 vào đa thức P(x) ta được:
\(P(0) = a.{( - 1)^2} + b.( - 1) + c = a + ( - b) + c = a - b + c\). Vậy \(P( - 1) = a - b + c\).
Cho đa thức A(x)= a(x)^2 + bx+c
tìm a,b,c biết A(0)=9;A(1)=20;A(-2)=7
A(0)=9 => a.0^2+b.0+c = 0
=> c=0
A(1)= a.1^2+b*1+0=20
=> a + b = 20(1)
A(-2)=7 => a(-2)^2+b*(-2)+0=7
=> 4a-2b=7
=> 2(2a-b)=7
=> 2a-b=3,5(2)
Từ (1) và (2) suy ra
a+b+2a-b=23,5
3a=23,5
=> a=47/6
=> b= 73/6
A(0) = 9 suy ra a . 0^2 + b * 0 + c = 0
Suy ra c = 0
A(1) = a . 1^2 + b*1 + 0 = 20
Suy ra a + b = 20 (1)
A(-2) = 7 suy ra a (-2)^2 + b * (-2) + 0 = 7
Suy ra 4a - 2b = 7
Suy ra 2( 2a - b )
Suy ra 2a - b = 3,5 (2)
Từ (1) và (2) suy ra a + b + 2a -b = 23,5
3a = 23,5
Suy ra a = 47/6
b = 73/6
sai r bạn ơi A(0)=9=>a*0+b*0+c=0=>c=9 chứ