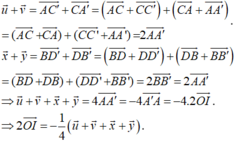cho hình bình hành ABCD , có tâm I(1;2) và các đường thẳng AB, BC,CD,DA lần lượt đi qua các đi qua các điểm M(0;1) ,N(4;2) P(-1;-1) và Q(0;3) . viết phương trình các đường thẳng chứa 4 cạnh của hình bình hành

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
GIÚP EM VỚI Ạ, CHIỀU NAY EM THI RỒI :(
Câu 5: Trong mặt phẳng toạ độ Oxy cho A(3;-1) ; B(-1;2) ; và I(1;1). Xác định toạ độ điểm C, D sao cho tứ giác ABCD là hình bình hành biết I là trong tâm tam giác ABC. Tìm toạ tâm O của hình bình hành ABCD
I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)
Đúng 1
Bình luận (0)
Cho hình bình hành EFGH có 4 đỉnh lần lượt nằm trên 4 cạnh của hình bình hành ABCD. Chứn minh rằng 2 hình bình hành này có cùng 1 tâm đối xứng
cho hình bình hành abcd, ở phía ngoài của hình bình hành vẽ 4 hình vuông có cạnh là các cạnh của hình bình hành. cmr tâm của các hình vuông là đỉnh của 1 hình vuông khác
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD tâm I có M là trung điểm DI. Chứng minh vectơ CM= 3CD+CB/4
cho hình bình hành ABCD có 4 đỉnh lần lượt nằm trên hình bình hành MNPQ. CM:2 hình bình hành này có cùng tâm đối xứng
Phần I: Trắc nghiệmCho hình hộp ABCD.ABCD có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt
A
C
→
u
→
,
C
A
→
v
→
,
B
D
→
x
→
,
D...
Đọc tiếp
Phần I: Trắc nghiệm
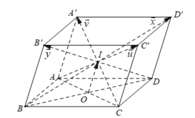
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt A C ' → = u → , C A ' → = v → , B D ' → = x → , D B ' → = y → . Khẳng định nào sau đây đúng?
A. 2 O I → = 1 2 u → + v → + x → + y →
B. 2 O I → = - 1 2 u → + v → + x → + y →
C. 2 O I → = 1 4 u → + v → + x → + y →
D. 2 O I → = - 1 4 u → + v → + x → + y →
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
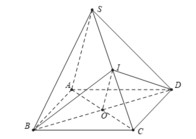
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây sai?
A. IO // mp(SAB) .
B. IO // mp(SAD).
C. mp (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác.
D. (IBD) ∩ (SAC).
Chọn C.
+) Ta có:
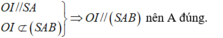
+) Ta có:
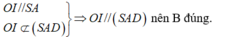
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.
Đúng 0
Bình luận (0)