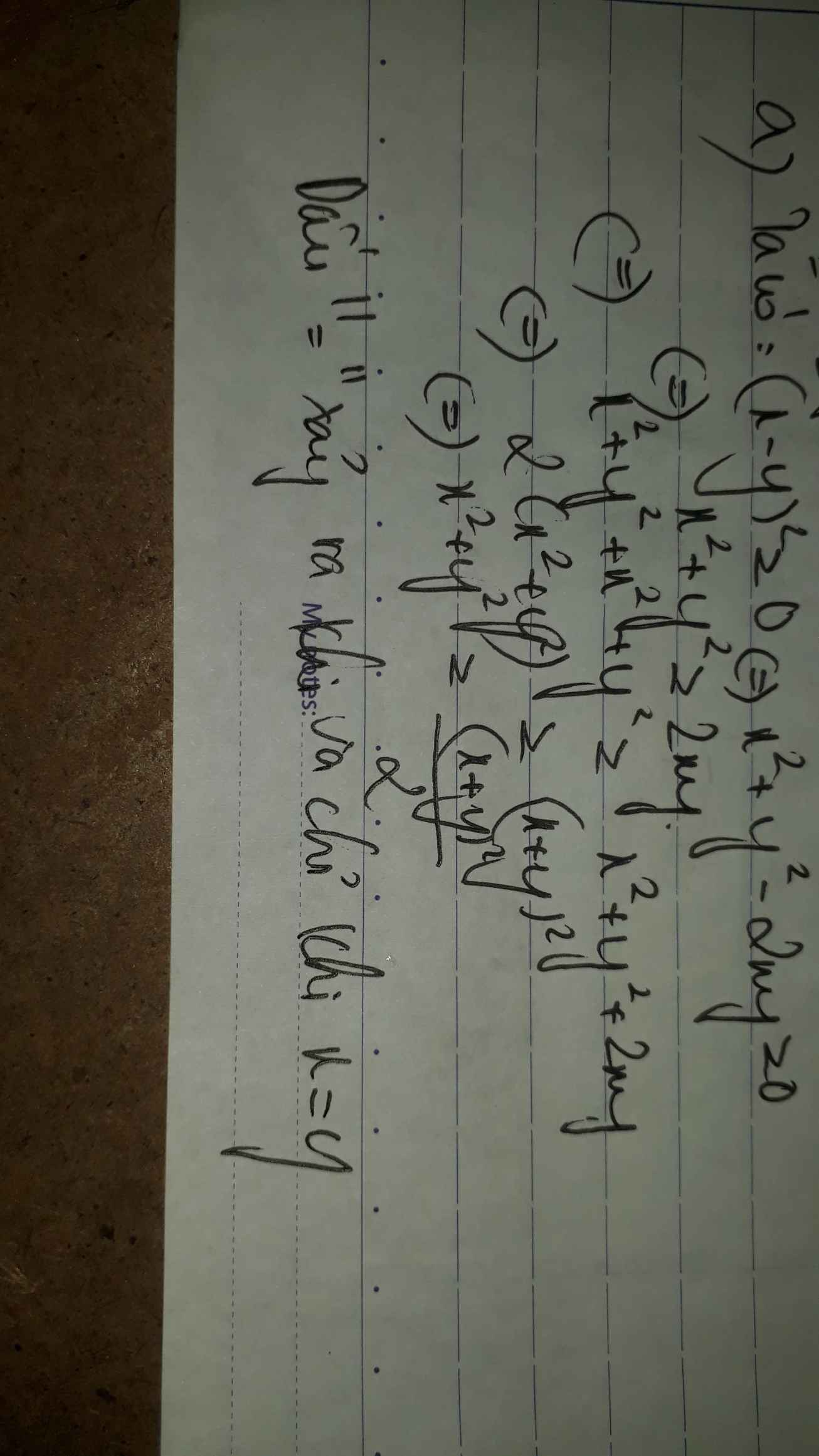\(\dfrac{x^2+1}{x}=\dfrac{x^2}{x}+\dfrac{1}{x}=x+\dfrac{1}{x}\)

Theo bất đẳng thức Cô - si, ta có:

\(x+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}=2\sqrt{1}=2\)

Vậy \(\dfrac{x^2+1}{x}\ge2\)

1 cách chứng minh khác (chứng minh tương đương)

\(\dfrac{x^2+1}{x}\ge2\\ \Leftrightarrow x^2+1\ge2x\\ \Leftrightarrow x^2-2x+1=\left(x-1\right)^2\ge0\left(\text{luôn đúng}\right)\)

Vậy BĐT ban đầu được chứng minh

a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)

b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)

\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)

\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)

\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)

a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\)

\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)

Điều kiện là \(xy\ne0\)

BĐT tương đương:

\(\left(\dfrac{x}{y}+\dfrac{y}{x}\right)^2-3\left(\dfrac{x}{y}+\dfrac{y}{x}\right)+2\ge0\)

\(\Leftrightarrow\left(\dfrac{x}{y}+\dfrac{y}{x}-1\right)\left(\dfrac{x}{y}+\dfrac{y}{x}-2\right)\ge0\)

\(\Leftrightarrow\dfrac{\left(x^2+y^2-xy\right)\left(x-y\right)^2}{x^2y^2}\ge0\) (luôn đúng)

Giải xàm tí ạ!\(VT-VP=\frac{1}{2}\left[\left(x^2-3x+1\right)^2+\left(y^2-3y+1\right)^2+\left(x-y\right)^2\left(5-x-y\right)\left(x+y-1\right)\right]\ge0\)

=> qed

??? KHang ơi! Sai rồi ? Tại sao VT - Vp = 1/2. Dòng thứ 2 ??? 

Nguyễn Linh Chi còn khúc dưới nữa mà cô, tại nó dài quá nên olm ko hiển thị hết trng một dòng. Mà bài đó em cũng làm xàm:)

Lời giải:

Nếu $x,y$ trái dấu: Ta thấy vế trái luôn lớn hơn $0$, còn vế phải sẽ nhỏ hơn $0$ do \(x,y\) trái dấu thì \(\frac{x}{y}; \frac{y}{x}< 0\)

Do đó \(\text{VT}> \text{VP}(1)\)

Nếu $x,y$ cùng dấu:

\(\frac{x^2}{y^2}+\frac{y^2}{x^2}+4-3\left(\frac{x}{y}+\frac{y}{x}\right)=\left(\frac{x}{y}+\frac{y}{x}\right)^2+2-3\left(\frac{x}{y}+\frac{y}{x}\right)\)

\(=t^2+2-3t=(t-1)(t-2)\) với \(t=\frac{x}{y}+\frac{y}{x}\)

Áp dụng BĐT Cô-si cho 2 số dương:

\(t=\frac{x}{y}+\frac{y}{x}\geq 2\sqrt{\frac{x}{y}.\frac{y}{x}}=2\)

\(\Rightarrow t-1>0; t-2\geq 0\Rightarrow (t-1)(t-2)\geq 0\)

Hay \(\frac{x^2}{y^2}+\frac{y^2}{x^2}+4\geq 3(\frac{x}{y}+\frac{y}{x})\) (2)

Từ $(1);(2)$ ta có đpcm

Dấu bằng xảy ra khi \(x=y\neq 0\)

Ta có:

\(VT=2+\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{z}{y}+\dfrac{y}{z}+\dfrac{x}{z}+\dfrac{z}{x}\)

Do đó ta chỉ cần chứng minh:

\(\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{y}+\dfrac{z}{x}+\dfrac{x}{z}\ge\dfrac{2\left(x+y+z\right)}{\sqrt[3]{xyz}}\)

Ta có:

\(\dfrac{x}{y}+\dfrac{x}{y}+1\ge3\sqrt[3]{\dfrac{x^2}{y^2}}\) 

Tương tự ...

Cộng lại ta có:

\(2\left(\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{y}+\dfrac{z}{x}+\dfrac{x}{z}\right)+6\ge3\left(\sqrt[3]{\dfrac{x^2}{y^2}}+\sqrt[3]{\dfrac{y^2}{x^2}}+\sqrt[3]{\dfrac{y^2}{z^2}}+\sqrt[3]{\dfrac{z^2}{y^2}}+\sqrt[3]{\dfrac{z^2}{x^2}}+\sqrt[3]{\dfrac{x^2}{z^2}}\right)\)

\(\Rightarrow\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{y}+\dfrac{z}{x}+\dfrac{x}{z}\ge\sqrt[3]{\dfrac{x^2}{y^2}}+\sqrt[3]{\dfrac{y^2}{x^2}}+\sqrt[3]{\dfrac{y^2}{z^2}}+\sqrt[3]{\dfrac{z^2}{y^2}}+\sqrt[3]{\dfrac{z^2}{x^2}}+\sqrt[3]{\dfrac{x^2}{z^2}}\)

Do đó ta chỉ cần chứng minh:

\(\sqrt[3]{\dfrac{x^2}{y^2}}+\sqrt[3]{\dfrac{y^2}{x^2}}+\sqrt[3]{\dfrac{y^2}{z^2}}+\sqrt[3]{\dfrac{z^2}{y^2}}+\sqrt[3]{\dfrac{z^2}{x^2}}+\sqrt[3]{\dfrac{x^2}{z^2}}\ge\dfrac{2\left(x+y+z\right)}{\sqrt[3]{xyz}}\)

\(\Leftrightarrow\left(\sqrt[3]{\dfrac{x}{y}}-\sqrt[3]{\dfrac{x}{z}}\right)^2+\left(\sqrt[3]{\dfrac{y}{x}}-\sqrt[3]{\dfrac{y}{z}}\right)^2+\left(\sqrt[3]{\dfrac{z}{x}}-\sqrt[3]{\dfrac{z}{y}}\right)^2\ge0\) (luôn đúng)