2100- (299+298+297+...+2+1)
Các bạn giúp mik vs, mik đang cần gấp
bài 2 : rút gọn
a ) A= 2100 - 2 99 + 298- 297 + ..... + 22-2
B ) A = 2 . 84 . 272 + 4 . 69 / 27 . 67 + 27 . 40 + 94
c) B= 45 . 94 - 2 . 64 / 210 . 38 + 68 .20
làm gấp giúp mik nhé
thanks các bạn ![]()
a: \(A=2^{100}-2^{99}+2^{98}-2^{97}+...+2^2-2\)
=>\(2A=2^{101}-2^{100}+2^{99}-2^{98}+...+2^3-2^2\)
=>\(2A+A=2^{101}-2^{100}+2^{99}-2^{98}+...+2^3-2^2+2^{100}-2^{99}+...+2^2-2\)
=>\(3A=2^{101}-2\)
=>\(A=\dfrac{2^{101}-2}{3}\)
b: Sửa đề: \(A=\dfrac{2\cdot8^4\cdot27^2+4\cdot6^9}{2^7\cdot6^7+2^7\cdot40\cdot9^4}\)
\(A=\dfrac{2\cdot2^{12}\cdot3^6+2^2\cdot2^9\cdot3^9}{2^7\cdot2^7\cdot3^7+2^7\cdot2^3\cdot5\cdot3^8}\)
\(=\dfrac{2^{11}\cdot3^6\left(2^3+3^3\right)}{2^{10}\cdot3^7\left(2^4+5\cdot3\right)}\)
\(=\dfrac{2}{3}\cdot\dfrac{4+27}{16+15}=\dfrac{2}{3}\)
c: \(B=\dfrac{4^5\cdot9^4-2\cdot6^4}{2^{10}\cdot3^8+6^8\cdot20}\)
\(=\dfrac{2^{10}\cdot3^8-2\cdot2^4\cdot3^4}{2^{10}\cdot3^8+2^8\cdot2^2\cdot5\cdot3^8}\)
\(=\dfrac{2^5\cdot3^4\left(2^5\cdot3^4-1\right)}{2^{10}\cdot3^8\left(1+5\right)}=\dfrac{1}{2^5\cdot3^4}\cdot\dfrac{32\cdot81-1}{6}\)
\(=\dfrac{2591}{2^6\cdot3^5}\)
Rút gọn mỗi biểu thức sau :
câu a) A=1+3+3^2+3^3+.........................+3^99 +3^100
câu b) B=2100-299+298-297+....-23+22-2+1
mấy cái (/ ) là luỹ thừa
giúp mình với mình đang cần ![]()
Tổng S = 1 + 2 + 3 + ... + 298 + 299 bằng...
giúp mik nhanh nha mik cần gấp
Số lượng số hạng:
\(\left(299-1\right):1+1=299\) (số hạng)
Tổng S là:
\(\left(299+1\right)\cdot299:2=44850\)
Số lượng số hạng:
\left(299-1\right):1+1=299(299−1):1+1=299 (số hạng)
Tổng S là:
\left(299+1\right)\cdot299:2=44850(299+1)⋅299:2=44850
Tính
A= 2100 - 299 - 298 - 297 - .......... - 22 - 2 - 1
\(A=2^{100}-\left(2^{99}+2^{98}+...+2+1\right)\)
Đặt \(B=2^{99}+2^{98}+...+2+1\)
\(\Rightarrow2B=2^{100}+2^{99}+...+2^2+2\)
\(\Rightarrow2B-B=2^{100}-1\Leftrightarrow B=2^{100}-1\)
\(\Rightarrow A=2^{100}-\left(2^{100}-1\right)=1\)
A=2100-299+298-297+...-23+22-2+1
HELP ME
\(A=2^{100}-2^{99}+2^{98}-2^{97}+....-2^3+2^2-2+1\\ A=\left(2^{100}+2^{98}+...+2\right)-\left(2^{99}+2^{97}+...+1\right)\)
Gọi \(\left(2^{100}+2^{98}+...+2\right)\)là B
\(B=\left(2^{100}+2^{98}+...+2\right)\\ 2B=2^{102}+2^{100}+.....+2^2\\ 2B-B=\left(2^{102}+2^{100}+.....+2^2\right)-\left(2^{100}+2^{98}+...+2\right)\\ B=2^{102}-2\)
Gọi \(\left(2^{99}+2^{97}+...+1\right)\) là C
\(C=\left(2^{99}+2^{97}+...+1\right)\\ 2C=2^{101}+2^{99}+....+2\\ 2C-C=\left(2^{101}+2^{99}+9^{97}+...+2\right)-\left(2^{99}+9^{97}+...+1\right)\\ C=2^{101}-1\)
\(A=B+C\\ =>A=2^{102}-2+2^{101}-1\\ A=2^{101}\left(2+1\right)-3\\ A=2^{101}\cdot3-3\\ A=3\cdot\left(2^{101}-1\right)\)
\(\dfrac{1}{2}A=2^{99}-2^{98}+...-1+\dfrac{1}{2}\\ \Rightarrow A-\dfrac{1}{2}A=2^{100}-\dfrac{1}{2}\\ \Rightarrow A=2^{101}-1\)
a, A= 2100 - 299 - 298 - 297 - ... - 2 -
tham khảo
https://olm.vn/hoi-dap/tim-kiem?q=A=2100-299-298-297-.........-22-2-1+.+t%C3%ADnh+A&id=52301
\(A=2^{100}-2^{99}-2^{98}-...-2\)
\(\Rightarrow-2A=-2^{101}+2^{100}+2^{99}+...+2^2\)
\(\Rightarrow A-2A=2^{100}-2^{99}-...-2-2^{101}+2^{100}+...2^2\)
\(\Rightarrow-A=2^{100}+2^{100}-2^{101}-2\)
\(\Rightarrow-A=-2\Rightarrow A=2\)
CMR :
2100 - 299 + 298 - 297 + ...... + 24 - 23 + 22 ⋮ 12
\(2^{100}-2^{99}+2^{98}-2^{97}+2^{96}-2^{95}+...+2^4-2^3+2^2\)
\(=\left(2^{100}-2^{99}+2^{98}\right)-\left(2^{97}-2^{96}+2^{95}\right)+...+\left(2^4-2^3+2^2\right)\)
\(=2^{96}\left(2^4-2^3+2^2\right)-2^{93}\left(2^4-2^3+2^2\right)+...+\left(2^4-2^3+2^2\right)\)
\(=12\left(2^{96}-2^{93}+...+1\right)⋮12\)
TÍNH C = 2100-299-298-....-2-1
Giúp vs. Thanks trc nhé
chẳng có qui luật gì cả. 1, 2, 3, 4...,298, 299 rồi sau đó là 2100 chẳng hợp gì cả
a, A = 1 + 2 + 22 + 23 + ... + 250 =
b, B = 1 + 3 + 32 + 33 + ... 3100 =
c, C = 5 + 52 + 53 + ... 530 =
d, D = 2100 = 299 + 298 - 297 + ... + 22 - 2
a) \(A=1+2+2^2+...+2^{50}\)
\(\Rightarrow2A=2+2^2+...+2^{51}\)
\(\Rightarrow A=2A-A=2+2^2+...+2^{51}-1-2-2^2-...-2^{50}=2^{51}-1\)
b) \(B=1+3+3^2+...+3^{100}\)
\(\Rightarrow3B=3+3^2+...+3^{101}\)
\(\Rightarrow2B=3B-B=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}=3^{101}-1\)
\(\Rightarrow B=\dfrac{3^{101}-1}{2}\)
c) \(C=5+5^2+...+5^{30}\)
\(\Rightarrow5C=5^2+5^3+...+5^{31}\)
\(\Rightarrow4C=5C-C=5^2+5^3+...+5^{31}-5-5^2-...-5^{30}=5^{31}-5\)
\(\Rightarrow C=\dfrac{5^{31}-5}{4}\)
d) \(D=2^{100}-2^{99}+2^{98}-...+2^2-2\)
\(\Rightarrow2D=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
\(\Rightarrow3D=2D+D=2^{101}-2^{100}+2^{99}-...+2^3-2^2+2^{100}-2^{99}+...+2^2-2=2^{101}-2\)
\(\Rightarrow D=\dfrac{2^{101}-2}{3}\)
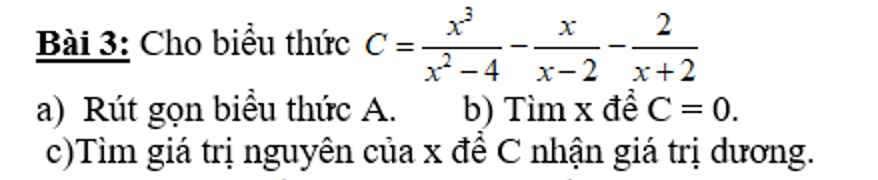
Các bạn giúp mik nhanh vs ạ! Huhu mik đang cần gấp lắm
\(C=\dfrac{x^3}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\)
\(=\dfrac{x^3-x\left(x+2\right)+2\left(x-2\right)}{x^2-4}\)
\(=\dfrac{x^3-x^2-2x+2x-4}{x^2-4}\)
\(=\dfrac{x^3-x^2-4}{x^2-4}\)
a,\(C=\dfrac{x^3}{x^2-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}\)
\(\Rightarrow C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{x^3-x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{\left(x^2-4\right)\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=\dfrac{\left(x-2\right)\left(x+2\right)\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow C=x-1\)
b, C=0\(\Rightarrow x-1=0\Rightarrow x=1\)
c, Để C nhận giá trị dương thì \(x-1\ge0\Rightarrow x\ge1\)