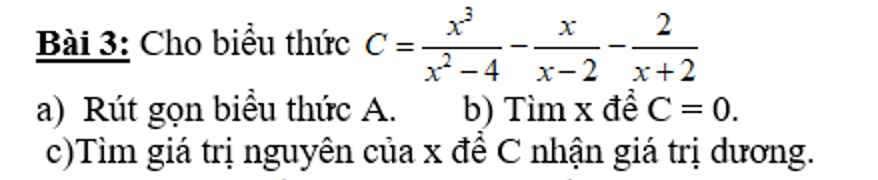Question

Các bạn giúp mik nhanh vs ạ! Huhu mik đang cần gấp lắm

Answer 1

Các bạn chỉ cần giúp mik câu c ạ

Answer 2

\(C=\dfrac{x^3}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\)

\(=\dfrac{x^3-x\left(x+2\right)+2\left(x-2\right)}{x^2-4}\)

\(=\dfrac{x^3-x^2-2x+2x-4}{x^2-4}\)

\(=\dfrac{x^3-x^2-4}{x^2-4}\)

Answer 3

a,\(C=\dfrac{x^3}{x^2-4}-\dfrac{x}{x-2}-\dfrac{2}{x+2}\)

\(\Rightarrow C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{x^3-x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{\left(x^2-4\right)\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=\dfrac{\left(x-2\right)\left(x+2\right)\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Rightarrow C=x-1\)

b, C=0\(\Rightarrow x-1=0\Rightarrow x=1\)

c, Để C nhận giá trị dương thì \(x-1\ge0\Rightarrow x\ge1\)

 

Answer 4

b) \(C=\dfrac{x^3-x^2-4}{x^2-4}=0\)

⇔ \(x^3-x^2-4=0\)

⇔ \(\left(x^3-2x^2\right)+\left(x^2-2x\right)+\left(2x-4\right)=0\)

⇔ \(\left(x-2\right)\left(x^2-x-2\right)=0\)

⇔ \(x=2\)