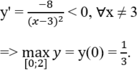Tìm giá trị lớn nhất của hàm số \(y=x^2-2x+3\) trên đoạn \(\left[0;4\right]\)

Những câu hỏi liên quan
tìm tất cả các giá trị nguyên âm của m để giá trị lớn nhất của hàm số
y=\(\left|x^2-2x-m\right|\) trên đoạn [-3;2] bằng 10
\(y=\left|x^2-2x-m\right|=-x^2+2x+m\)
\(\left(nếu:x^2-2x-m< 0\right)\)
\(f\left(x\right)=-x^2+2x+m\Rightarrow x=\dfrac{-b}{2a}=1\in\left[-3;2\right]\)
\(f\left(-3\right)=m-15\)
\(f\left(1\right)=m+1\)
\(f\left(2\right)=m\Rightarrow f\left(-3\right)< f\left(2\right)< f\left(1\right)\)
\(\Rightarrow max_{f\left(x\right)}=m+1=10\Leftrightarrow m=9\)
\(do..m< 0\Rightarrow m=9\left(ktm\right)\)
\(\Rightarrow không\) \(có\) \(giá\) \(trị\) \(m\) \(thỏa\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=\sqrt{x-1}+x^2-2x\)
a, Xét sự biến thiên của hàm số đã cho trên [ 1;+\(\infty\))
b, Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn \(\left[2;5\right]\)
please help me
i need it now
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
e
x
2
-
2
x
+
3
trên đoạn [0 ; 2] là: A .
e
3
-e B.
e
3
+
e
2...
Đọc tiếp
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = e x 2 - 2 x + 3 trên đoạn [0 ; 2] là:
A . e 3 -e
B. e 3 + e 2
C . e 3
D. e 3 +e
Tìm giá trị lớn nhất của hàm số \(y=f\left(x\right)=sin^2x+4sinx-5\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
A. \(-5\)
B. \(5\)
C. \(1\)
D. \(0\)
\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)
\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)
\(f'\left(x\right)=0\)
=>\(cosx\left(sinx+2\right)=0\)
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)
nên \(x=\dfrac{\Omega}{2}\)
\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)
=1+4-5=0
\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)
=>Chọn D
Đúng 0
Bình luận (1)
Tìm tất cả giá trị m để giá trị lớn nhất của hàm số:1/ ydfrac{2x+m}{x+1} trên left[0;1right] bằng 2.2/ yleft|x^3-3x^2+mright| trên left[0;3right] bằng 5.3/ yleft|dfrac{x^2+mx+m}{x+1}right| trên left[1;2right] bằng 2.4/ yleft|dfrac{1}{4}x^4-dfrac{19}{2}x^2+30x+m-20right| trên left[0;2right] không vượt quá 20.
Đọc tiếp
Tìm tất cả giá trị \(m\) để giá trị lớn nhất của hàm số:
1/ \(y=\dfrac{2x+m}{x+1}\) trên \(\left[0;1\right]\) bằng 2.
2/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 5.
3/ \(y=\left|\dfrac{x^2+mx+m}{x+1}\right|\) trên \(\left[1;2\right]\) bằng 2.
4/ \(y=\left|\dfrac{1}{4}x^4-\dfrac{19}{2}x^2+30x+m-20\right|\) trên \(\left[0;2\right]\) không vượt quá 20.
Cho hàm số y=\(x^2-2x-3\). Tìm giá trị lớn nhất của hàm số với \(x\in\left[-3;4\right]\).
Lời giải:
$x^2-2x-3=x(x+3)-5(x+3)+12=(x+3)(x-5)+12$
Vì $x\in [-3;4]$ nên $x+3\geq 0; x-5< 0$
$\Rightarrow x^2-2x-3=(x+3)(x-5)+12\leq 12$
Vậy GTLN của hàm số là $12$ khi $x=-3$
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
y
3
x
-
1
x
-
3
trên đoạn [0; 2] A. -1/3 . B. -5 C. 5 D. 1/3
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 3 x - 1 x - 3 trên đoạn [0; 2]
A. -1/3 .
B. -5
C. 5
D. 1/3
Giá trị lớn nhất của hàm số y = x ( 5 - 2 x ) 2 trên [0; 3] là:
A. 0
B. 125 27
C. 250 27
D. 250 3
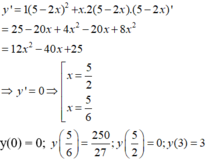
Vậy GTLN của hàm số trên [0; 3] là 250 27 đạt được khi x = 5/6. Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hàm số f(x)
2
x
+
m
x
+
1
với m là tham số thực. Tìm tất cả các giá trị của m 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3. A. 1m 3 B. m
∈
(
1
;
3
5
-
4
)
C....
Đọc tiếp
Cho hàm số f(x) = 2 x + m x + 1 với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
A. 1<m< 3
B. m ∈ ( 1 ; 3 5 - 4 )
C. m ∈ ( 1 ; 5 )
D. 1<m≤ 4
+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.
Đúng 0
Bình luận (0)