Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi V 1  là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′,  V 2  là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích V 1 V 2  là

A. 6

B. 2

C. 8

D. 4

Cho hai đường tròn (O;4cm), (I;2cm) cắt nhau tại hai điểm phân biệt A, B sao cho OAI ≠ 90^o. Tiếp tuyến của đường tròn (O) tại A cắt đường tròn (I) tại C khác A.Tiếp tuyến của đường tròn (I) tại A cắt đường tròn (O) tại D khác A. Gọi E là giao điểm của AB và CD. Gọi P, Q lần lượt là trung điểm của AD, CD. Chứng minh :

a) Hai tam giác APQ, ABC đồng dạng

b) ED = 4EC

giúp em bài này với ạ.

Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A′BD có thể tích bằng

A. 2 3 πa 3 27

B.  3 πa 3 8

C.  3 a 3 27

D.  πa 3 6

Cho △ABC. Vẻ A' đối xứng A qua C, B' đối xứng B qua A, C' đối xứng C qua B. Gọi D là trung điểm AC, D' là trrung điểm A'C'.

a, C/m ABDD' là hình bình hành

b, Gọi O là giao của trung tuyến BD và B'D', M là trung điểm OB; N là trung điểm OB'. C/m DD'MN là hình bình hành.

c, C/m O là trực tâm △ABC

Các bạn vẽ hình rồi giải giúp mik nha. Mik đang cần gấp

Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng

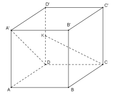
A.  10 5

B.  4 5

C.  10 10

D.  2 5

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Từ M vẽ 2 tiếp tuyến MA, MB (A,B là tiếp điểm). Đường thẳng qua M cắt đường tròn (O) tại C, D (MC<MD) sao cho điểm O nằm trong tam giác BCD. Vẽ đường kính CE của đường tròn (O). Gọi S là giao điểm của EA và BC

a) Cm tứ giác MAOB nội tiếp và OM vuông góc AB

b) Cm tam giác OAM đồng dạng CAS

c) Cm tam giác OAC và MAS đồng dạng và tam giác MAS cân

d) Gọi N là giao điểm của MO và AE. Cm tứ giác BSMN nội tiếp và ND vuông góc AD